某机场为了方便旅客换乘,计划在一、二层之间安装电梯,截面设计图如图所示,已知两层 AD与 BC平行,层高 AB为8米, A、 D间水平距离为5米,∠ ACB=21.5° 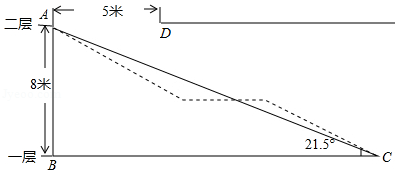
(1)通过计算说明身高2.4米的人在竖直站立的情况下,搭乘电梯在 D处会不会碰到头部;
(2)若采用中段加平台设计(如图虚线所示),已知平台 MN∥ BC,且 AM段和 NC段的坡度均为1:2(坡度是指坡面的铅直高度与水平宽度的比),求平台 MN的长度.
(参考数据:sin21.5°= ,cos21.5°= ,tan21.5°= )
如图:矩形ABCD中,AB=8,BC=6,请在下图中画出面积不相等的三个菱形大致图形,使菱形的顶点都在矩形的边上,并直接写出你画的菱形的边长.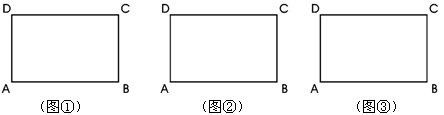
图①边长=; 图②边长=;图③边长=;
此题中是否存在满足条件的面积最大的菱形?(填“存在”或“不存在”).
元旦期间某班组织学生到竹海进行社会实践活动.下面是班主任与旅行社的一段通话记录:
班主任:请问组团到马山每人收费是多少?
导游:您好!如果人数不超过30人,人均收费100元(含门票).
班主任:超过30人怎样优惠呢?
导游:如果超过30人,每增加1人,人均费用少2元,但人均费用不能低于72元哟.
该班按此收费标准组团参观后,共支付给旅行社3150元.根据上述情景,请你帮班主任统计一下该班这次去参观的学生人数?
如图所示:将□ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F,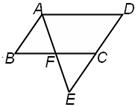
①、求证:△ABF≌△ECF;②、若AE=AD,连接AC、BE.求证:四边形ABEC是矩形.
如图所示:工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10cm,测得钢珠顶端离零件表面的距离为8cm,则这个小圆孔的宽口AB的长度为多少?
解方程:①、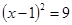 ;②、
;②、