【问题情景】
利用三角形的面积相等来求解的方法是一种常见的等积法,此方法是我们解决几何问题的途径之一.
例如:张老师给小聪提出这样一个问题:
如图1,在△ ABC中, AB=3, BC=6,问△ ABC的高 AD与 CE的比是多少?
小聪的计算思路是:
根据题意得: S △ ABC= BC• AD= AB• CE.
从而得2 AD= CE,∴ =
请运用上述材料中所积累的经验和方法解决下列问题:
(1)【类比探究】
如图2,在▱ ABCD中,点 E、 F分别在 AD, CD上,且 AF= CE,并相交于点 O,连接 BE、 BF,
求证: BO平分角 AOC.
(2)【探究延伸】
如图3,已知直线 m∥ n,点 A、 C是直线 m上两点,点 B、 D是直线 n上两点,点 P是线段 CD中点,且∠ APB=90°,两平行线 m、 n间的距离为4.求证: PA• PB=2 AB.
(3)【迁移应用】
如图4, E为 AB边上一点, ED⊥ AD, CE⊥ CB,垂足分别为 D, C,∠ DAB=∠ B, AB= , BC=2, AC= ,又已知 M、 N分别为 AE、 BE的中点,连接 DM、 CN.求△ DEM与△ CEN的周长之和.

已知BD垂直平分AC,∠BCD=∠ADF,AF⊥AC,
(1)证明四边形ABDF是平行四边形;
(2)若AF=DF=5,AD=6,求 的值.
的值.
已知⊙O的直径为10,点A,点B,点C在⊙O上,∠CAB的平分线交⊙O于点D.
(1)如图①,若BC为⊙O的直径,AB=6,求AC,BD,CD的长;
(2)如图②,若∠CAB=60°,求BD的长.
某班同学分三组进行数学活动,对七年级400名同学最喜欢喝的饮料情况,八年级300名同学零花钱的最主要用途情况,九年级300名同学完成家庭作业时间情况进行了全面调查,并分别用扇形图、频数分布直方图、表格来描述整理得到的数据
九年级同学家庭作业时间情况统计表
根据以上信息,请回答下列问题:
(1)七年级400名同学中最喜欢喝“冰红茶”的人数是多少;
(2)补全八年级300名同学中零花钱的最主要用途情况频数分布直方图;
(3)九年级300名同学中完成家庭作业的平均时间大约是多少小时?(结果保留一位小数)
已知抛物线y=ax2+bx+c经过 (-1,0),
(-1,0), (2,0),
(2,0), (0,2)三点.
(0,2)三点.
(1)求这条抛物线的解析式;
(2)如图①,点P是第一象限内此抛物线上的一个动点,当点P运动到什么位置时,四边形ABPC的面积最大?求出此时点P的坐标;
(3)如图②,设线段AC的垂直平分线交x轴于点E,垂足为D,M为抛物线的顶点,那么在直线DE上是否存在一点G,使△CMG的周长最小?若存在,请求出点G的坐标;若不存在,请说明理由.
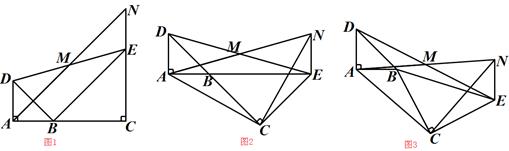
如图1,已知△BAD和△BCE均为等腰直角三角形,∠BAD=∠BCE=90°,点M为DE的中点.过点E与AD平行的直线交射线AM于点N.
(1)当A,B,C三点在同一直线上时(如图1),求证:M为AN的中点;
(2)将图1中△BCE绕点B旋转,当A,B,E三点在同一直线上时(如图2),求证:△CAN为等腰直角三角形;
(3)将图1中△BCE绕点B旋转到图3的位置时,(2)中的结论是否仍然成立?若成立,试证明之;若不成立,请说明理由.