在平面直角坐标系 xOy中，抛物线 y＝ ax 2+ bx+2过点 A（﹣2，0）， B（2，2），与 y轴交于点 C．
（1）求抛物线 y＝ ax 2+ bx+2的函数表达式；
（2）若点 D在抛物线 y＝ ax 2+ bx+2的对称轴上，求△ ACD的周长的最小值；
（3）在抛物线 y＝ ax 2+ bx+2的对称轴上是否存在点 P，使△ ACP是直角三角形？若存在直接写出点 P的坐标，若不存在，请说明理由．
作一直线，将下图分成面积相等的两部分（保留作图痕迹）．
如图，四边形ABCD是平行四边形，
，BD⊥AD，求BC，CD及OB的长.
某中学为了了解全校的耗电情况，抽查了10天中全校每天的耗电量，数据如下表：
| 千瓦时 |
90 |
93 |
102 |
113 |
114 |
120 |
| 天数 |
1 |
1 |
2 |
3 |
1 |
2 |
（1）写出上表中数据的众数和平均数．
（2）根据上题获得的数据，估计该校一个月的耗电量（按30天计算）．
（3）若当地每千瓦时电的价格是0．5元，写出该校应付电费y（元）与天数
（取正整数，单位：天）的函数关系式．
如图表示一个正比例函数与一个一次函数的图象，它们交于点A（4，3），一次函数的图象与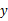
轴交于点B，且OA=OB，求这两个函数的关系式及两直线与
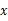轴围成的三角形的面积.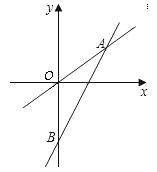 
“种粮补贴”惠农政策的出台，大大激发了农民的种粮积极性，某粮食生产专业户去年计划生产小麦和玉米共18吨，实际生产了20吨，其中小麦超产12％，玉米超产10％，该专业户去年实际生产小麦、玉米各多少吨？