如图，矩形OABC的两边OA，OC分别在x轴和y轴的正半轴上-优题课

如图，矩形OABC的两边OA，OC分别在x轴和y轴的正半轴上，点B的坐标为（ $4 \sqrt{3}, 4$ ），点D在CB上，且CD：DB＝2：1，OB交AD于点E．平行于x轴的直线l从原点O出发，以每秒1个单位长度的速度沿y轴向上平移，到C点时停止；l与线段OB，AD分别相交与M，N两点，以MN为边作等边△MNP（点P在线段MN的下方）．设直线l的运动时间为t（秒），△MNP与△OAB重叠部分的面积为S（平分单位）．

（1）直接写出点E的坐标；

（2）求S与t的函数关系式；

（3）是否存在某一时刻t，使得 $S = \frac{1}{2} S_{ΔABD}$ 成立？若存在，请求出此时t的值；若不存在，请说明理由．

科目数学题型解答题难度较难

知识点：解直角三角形相似三角形的判定与性质矩形的性质四边形综合题

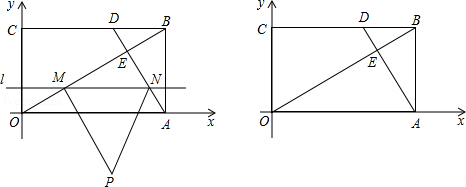
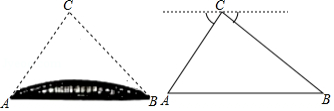
某校“综合与实践”小组采用无人机辅助的方法测量一座桥的长度．如图，桥 $AB$ 是水平并且笔直的，测量过程中，小组成员遥控无人机飞到桥 $AB$ 的上方120米的点 $C$ 处悬停，此时测得桥两端 $A$ ， $B$ 两点的俯角分别为 $60 °$ 和 $45 °$ ，求桥 $AB$ 的长度．

先化简，再求值： $(1 - \frac{x + 1}{x^{2} - 2 x + 1}) \div \frac{x - 3}{x - 1}$ ，其中 $x$ 是16的算术平方根．

发现规律

（1）如图①， $ΔABC$ 与 $ΔADE$ 都是等边三角形，直线 $BD$ ， $CE$ 交于点 $F$ ．直线 $BD$ ， $AC$ 交于点 $H$ ．求 $∠ BFC$ 的度数．

（2）已知： $ΔABC$ 与 $ΔADE$ 的位置如图②所示，直线 $BD$ ， $CE$ 交于点 $F$ ．直线 $BD$ ， $AC$ 交于点 $H$ ．若 $∠ ABC = ∠ ADE = α$ ， $∠ ACB = ∠ AED = β$ ，求 $∠ BFC$ 的度数．

应用结论

（3）如图③，在平面直角坐标系中，点 $O$ 的坐标为 $(0, 0)$ ，点 $M$ 的坐标为 $(3, 0)$ ， $N$ 为 $y$ 轴上一动点，连接 $MN$ ．将线段 $MN$ 绕点 $M$ 逆时针旋转 $60 °$ 得到线段 $MK$ ，连接 $NK$ ， $OK$ ．求线段 $OK$ 长度的最小值．

已知，在平面直角坐标系中，抛物线 $y = x^{2} - 2 mx + m^{2} + 2 m - 1$ 的顶点为 $A$ ．点 $B$ 的坐标为 $(3, 5)$ ．

（1）求抛物线过点 $B$ 时顶点 $A$ 的坐标；

（2）点 $A$ 的坐标记为 $(x, y)$ ，求 $y$ 与 $x$ 的函数表达式；

（3）已知 $C$ 点的坐标为 $(0, 2)$ ，当 $m$ 取何值时，抛物线 $y = x^{2} - 2 mx + m^{2} + 2 m - 1$ 与线段 $BC$ 只有一个交点．

小伟和小梅两位同学玩掷骰子的游戏，两人各掷一次均匀的骰子．以掷出的点数之差的绝对值判断输赢．若所得数值等于0，1，2，则小伟胜；若所得数值等于3，4，5，则小梅胜．

（1）请利用表格分别求出小伟、小梅获胜的概率；

（2）判断上述游戏是否公平．如果公平，请说明理由；如果不公平，请利用表格修改游戏规则，以确保游戏的公平性．

试卷网试题网古诗词网作文网范文网