如图,在平面直角坐标系xOy中,直线y=2x+4与y轴交于A点,与x轴交于B点,抛物线 过A、B两点,与x轴另一交点为C.
(1)求抛物线解析式及C点坐标.
(2)向右平移抛物线C1,使平移后的抛物线C2恰好经过△ABC的外心,抛物线C1、C2相交于点D,求四边形AOCD的面积.
(3)已知抛物线C2的顶点为M,设P为抛物线C1对称轴上一点,Q为抛物线C1上一点,是否存在以点M、Q、P、B为顶点的四边形为平行四边形?若存在,直接写出P点坐标;不存在,请说明理由.

观察下面的点阵图形和与之相对应的等式,探究其中的规律:
(1)请你在④和⑤后面的横线上分别写出相对应的等式:
通过猜想,写出与第n个图形相对应的等式:____________________________, 并说明你猜想的正确性.
计算:
(1)-4-(-19)+(-24);
(2)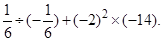
在数轴上把下列各数表示出来,并用“<”连接各数. ,
,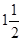 ,
, ,-
,-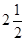 ,
,
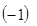 ,
,
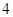 .
.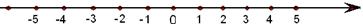
(本题14分)已知锐角△ABC中,CD、BE分别是AB、AC边上的高,M是线段BC的中点,连接DM、EM.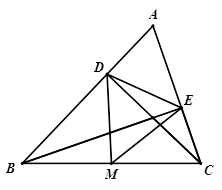
(1)若DE=3,BC=8,求△DME的周长;
(2)若∠A=60°,求证:∠DME=60°;
(3)若BC2=2DE2,求∠A的度数.
(本题12分)如图1,在等边△ABC中,点E从顶点A出发,沿AB的方向运动,同时,点D从顶点B出发,沿BC的方向运动,它们的速度相同,当点E到达点B时, D、E两点同时停止运动.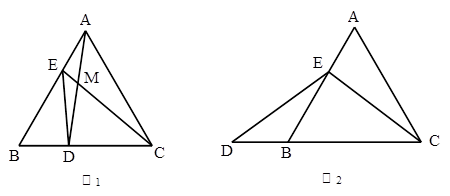
(1)求证:CE=AD;
(2)连接AD、CE交于点M,则在D、E运动的过程中,∠CMD变化吗?若变化,则说明理由;若不变,则求出它的度数;
(3)如图2,若点D从顶点B出发后,沿BC相反的方向运动,其它条件不变. 求证:CE=DE.