如图,AB是半圆O的直径,点P是BA延长线上一点,PC是⊙O的切线,切点为C,过点B作BD⊥PC交PC的延长线于点D,连接BC.求证:
(1)∠PBC=∠CBD;
(2)BC2=AB•BD.

如图,小红用一张长方形纸片ABCD进行折纸,已知该纸片宽AB为8cm,长BC为10cm.当小红折叠时,顶点D落在BC边上的点F处(折痕为AE).想一想,此时EC有多长?用你学过的方法进行解释.
已知抛物线y=ax2+bx+c经过A(﹣1,0)、B(2,0)、C(0,2)三点.
(1)求这条抛物线的解析式;
(2)如图一,点P是第一象限内此抛物线上的一个动点,当点P运动到什么位置时,四边形ABPC的面积最大?求出此时点P的坐标;
(3)如图二,设线段AC的垂直平分线交x轴于点E,垂足为D,M为抛物线的顶点,那么在直线DE上是否存在一点G,使△CMG的周长最小?若存在,请求出点G的坐标;若不存在,请说明理由.
如图,在Rt△ABC中,∠BAC=90°,∠B=60°,BC=16cm,AD是斜边BC上的高,垂足为D,BE=1cm.点M从点B出发沿BC方向以1cm/s的速度运动,点N从点E出发,与点M同时同方向以相同的速度运动,以MN为边在BC的上方作正方形MNGH.点M到达点D时停止运动,点N到达点C时停止运动.设运动时间为t(s).
(1)当t为何值时,点G刚好落在线段AD上?
(2)设正方形MNGH与Rt△ABC重叠部分的图形的面积为S,当重叠部分的图形是正方形时,求出S关于t的函数关系式并写出自变量t的取值范围.
(3)设正方形MNGH的边NG所在直线与线段AC交于点P,连接DP,当t为何值时,△CPD是等腰三角形?
为推进郴州市创建国家森林城市工作,尽快实现“让森林走进城市,让城市拥抱森林”的构想,今年三月份,某县园林办购买了甲、乙两种树苗共1000棵,其中甲种树苗每棵40元,乙种树苗每棵50元,据相关资料表明:甲、乙两种树苗的成活率分别为85%和90%.
(1)若购买甲、乙两种树苗共用去了46500元,则购买甲、乙两种树苗各多少棵?
(2)若要使这批树苗的成活率不低于88%,则至多可购买甲种树苗多少棵?
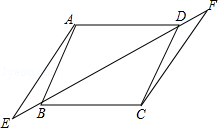
如图,已知四边形ABCD是平行四边形,点E、B、D、F在同一直线上,且BE=DF.求证:AE=CF.