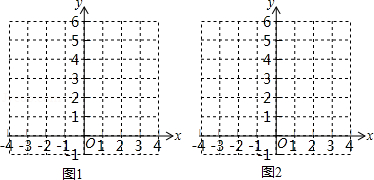
如图1，在平面直角坐标系xOy中，点A的坐标为（0，1），取一点B（b，0），连接AB，作线段AB的垂直平分线l1，过点B作x轴的垂线l2，记l1，l2的交点为P．
（1）当b＝3时，在图1中补全图形（尺规作图，不写作法，保留作图痕迹）；
（2）小慧多次取不同数值b，得出相应的点P，并把这些点用平滑的曲线连接起来发现：这些点P竟然在一条曲线L上！
①设点P的坐标为（x，y），试求y与x之间的关系式，并指出曲线L是哪种曲线；
②设点P到x轴，y轴的距离分别是d1，d2，求d1+d2的范围，当d1+d2＝8时，求点P的坐标；
③将曲线L在直线 下方的部分沿直线y＝2向上翻折，得到一条“W”形状的新曲线，若直线 与这条“W”形状的新曲线有4个交点，直接写出k的取值范围．
已知关于x的一元二次方程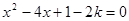
有两个不等的实根，（1）求k的取值范围；
（2）若k取小于1的整数，且此方程的解为整数，则求出此方程的两个整数根；
（3）在（2）的条件下，二次函数
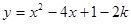与x轴交于A、B两点（A点在B点的左侧），D点在此抛物线的对称轴上，若
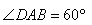，求D点的坐标。
如图1，若将△AOB绕点O逆时针旋转180°得到△COD，则△AOB≌△COD．此时，我们称△AOB与△COD为“8字全等型”．借助“8字全等型”我们可以解决一些图形的分割与拼接问题．例如：图2中，△ABC是锐角三角形且AC＞AB，点E为AC中点，F为BC上一点且BF≠FC（F不与B、C重合），沿EF将其剪开，得到的两块图形恰能拼成一个梯形．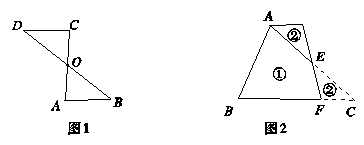
请分别按下列要求用直线将图2中的△ABC重新进行分割，画出分割线及拼接后的图形．
（1）在图3中将△ABC沿分割线剪开，使得到的两块图形恰能拼成一个平行四边形；
（2在图4中将△ABC沿分割线剪开，使得到的三块图形恰能拼成一个矩形，且其中的两块为直角三角形；
（3在图5中将△ABC沿分割线剪开，使得到的三块图形恰能拼成一个矩形，且其中的一块为锐角三角形．
已知：如图，AB是⊙O的直径，BC是弦，OD⊥BC于点F，交⊙O于点D，连接AD、CD，∠E=∠ADC.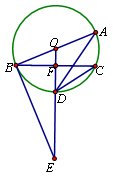
（1）求证：BE是⊙O的切线；
（2）若BC=6，tanA =
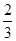，求⊙O的半径.
一个袋中有3张形状大小完全相同的卡片，编号为1、2、3，先任取一张，再从剩下的两张中任取一张.请你用列举法（画树状图或列表的方法）求取出的两张卡片上的数字之和为5的概率.
如图, 小明想测量某建筑物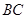
的高,站在点
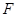处,看建筑物的顶端
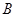,测得仰角为
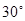,再往建筑物方向
前行
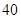米到达点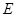
处,看到其顶端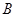,测得仰角为
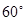,求建筑物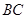的长( 结果精确到
，
).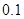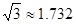