阅读下列材料:
如图1,在△ ABC中,∠ A、∠ B、∠ C所对的边分别为 a、 b、 c,可以得到:
S △ ABC= absin C= acsin B= bcsin A
证明:过点 A作 AD⊥ BC,垂足为 D.
在Rt△ ABD中,sin B=
∴ AD= c•sin B
∴ S △ ABC= a• AD= acsin B
同理: S △ ABC= absin C
S △ ABC= bcsin A
∴ S △ ABC= absin C= acsin B= bcsin A
(1)通过上述材料证明:
(2)运用(1)中的结论解决问题:
如图2,在△ ABC中,∠ B=15°,∠ C=60°, AB=20 ,求 AC的长度.
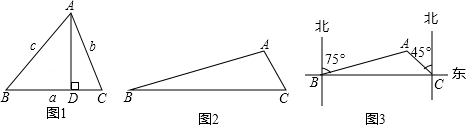
(3)如图3,为了开发公路旁的城市荒地,测量人员选择 A、 B、 C三个测量点,在 B点测得 A在北偏东75°方向上,沿笔直公路向正东方向行驶18 km到达 C点,测得 A在北偏西45°方向上,根据以上信息,求 A、 B、 C三点围成的三角形的面积.
(本题参考数值:sin15°≈0.3,sin120°≈0.9, ≈1.4,结果取整数)
如图,已知CD是⊙O的直径,AC⊥CD,垂足为C,弦DE∥OA,直线AE、CD相交于点B.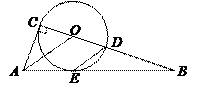 (1)求证:直线AB是⊙O的切线.
(1)求证:直线AB是⊙O的切线.
(2)当AC=1,BE=2,求tan∠OAC的值.
南宁市五象新区有长24000m的新建道路要铺上沥青.
(1)写出铺路所需时间t(天)与铺路速度v(m/天)的函数关系式.
(2)负责铺路的工程公司现有的铺路机每天最多能铺路400m,预计最快多少天可以完成铺路任务?
(3)为加快工程进度,公司决定投入不超过400万元的资金,购进10台更先进的铺路机.现有甲、乙两种机器可供选择,其中每种机器的价格和日铺路能力如下表.在原有的铺路机连续铺路40天后,新购进的10台机器加入铺路,公司要求至少比原来预计的时间提前10天完成任务.问有哪几种方案?请你通过计算说明选择哪种方案所用资金最少.
| 甲 |
乙 |
|
| 价格(万元/台) |
45 |
25 |
| 每台日铺路能力(m) |
50 |
30 |
某校宣传栏中公示了担任下学期七年级班主任的12位老师的情况(见下表),小凤准备到该校就读七年级,请根据表中信息帮小凤进行如下统计分析:
| 姓名 |
性别 |
年龄 |
学历 |
职称 |
姓名 |
性别 |
年龄 |
学历 |
职称 |
|
| 王雄辉 |
男 |
35 |
本科 |
高级 |
蔡波 |
男 |
45 |
大专 |
高级 |
|
| 李红 |
男 |
40 |
本科 |
中级 |
李凤 |
女 |
27 |
本科 |
初级 |
|
| 刘梅英 |
女 |
40 |
中专 |
中级 |
孙焰 |
男 |
40 |
大专 |
中级 |
|
| 张英 |
女 |
43 |
大专 |
高级 |
彭朝阳 |
男 |
30 |
大专 |
初级 |
|
| 刘元 |
男 |
50 |
中专 |
中级 |
龙妍 |
女 |
25 |
本科 |
初级 |
|
| 袁桂 |
男 |
30 |
本科 |
初级 |
杨书 |
男 |
40 |
本科 |
中级 |
(1)该校下学期七年级班主任老师年龄的众数是多少?
(2)在图7(1)中,将反映老师学历情况的条形统计图补充完整;
(3)在图7(2)中,标注扇形统计图中表示老师职称为初级和高级的百分比;
(4)小凤到该校就读七年级,班主任老师是女老师的概率是多少?
 |
观察下列算式:
①1 × 3 - 22 =" 3" - 4 = -1
② 2 × 4 - 32 =" 8" - 9 = -1
③ 3 × 5 - 42 =" 15" - 16 = -1
④
……
(1)请你按以上规律写出第4个算式;
(2)把这个规律用含字母的式子表示出来;
(3)你认为(2)中所写出的式子一定成立吗?并说明理由.
若△ABC和△ADE均为等边三角形,M、N分别是BE、CD的中点.
(1)当△ADE绕A点旋转到如图①的位置时,求证:CD=BE,△AMN是等边三角形;
(2) 如图②,当∠EAB=30°,AB=12,AD= 时,求AM的长.
时,求AM的长.
 |
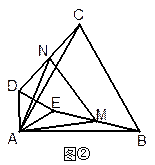 |
||