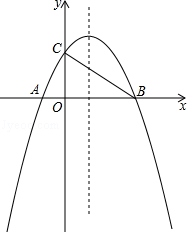
如图，在平面直角坐标系中，已知抛物线 y＝ ax 2+ bx+2（ a≠0）与 x轴交于 A（﹣1，0）， B（3，0）两点，与 y轴交于点 C，连接 BC．
（1）求该抛物线的解析式，并写出它的对称轴；
（2）点 D为抛物线对称轴上一点，连接 CD、 BD，若∠ DCB＝∠ CBD，求点 D的坐标；
（3）已知 F（1，1），若 E（ x， y）是抛物线上一个动点（其中1＜ x＜2），连接 CE、 CF、 EF，求△ CEF面积的最大值及此时点 E的坐标．
（4）若点 N为抛物线对称轴上一点，抛物线上是否存在点 M，使得以 B， C， M， N为顶点的四边形是平行四边形？若存在，请直接写出所有满足条件的点 M的坐标；若不存在，请说明理由．
在数轴上表示不等式的解集：x≥－3.5 
如图，在直角坐标系中，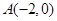
，
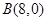，以AB为直径作半⊙P交y轴于M，以AB为一边作正方形ABCD.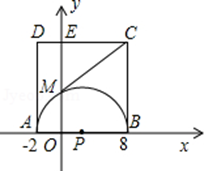
（1）求C、M两点的坐标；
（2）连结CM，试判断直线CM是否与⊙P相切？说明你的理由；
（3）在x轴上是否存在一点Q，使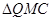
周长最小？若存在，求出Q坐标及最小周长，若不存在，请说明理由.
已知：如图，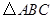
中，
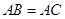，以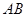
为直径的⊙O交
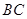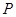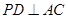于点
，
于点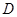
．
（1）求证：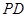
是⊙O的切线；
（2）若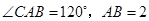
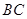，求的值．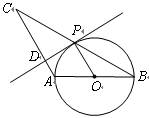
观察下列等式：
第1个等式：
；
第2个等式： 
；
第3个等式： 
；
第4个等式： 
；
……
请解答下列问题：
（1）按以上规律列出第5个等式：
= =；
（2）用含有n的代数式表示第n个等式：
= = （n为正整数）；
（3）求
的值．
兴隆镇某养鸡专业户准备建造如图所示的矩形养鸡场，要求长与宽的比为2：1，在养鸡场内，沿前侧内墙保留3m宽的走道，其他三侧内墙各保留1m宽的走道，当矩形养鸡场长和宽各为多少时，鸡笼区域面积是288
？