已知二次函数 y= ax 2﹣ bx+ c且 a= b,若一次函数 y= kx+4与二次函数的图象交于点 A(2,0).
(1)写出一次函数的解析式,并求出二次函数与 x轴交点坐标;
(2)当 a> c时,求证:直线 y= kx+4与抛物线 y= ax 2﹣ bx+ c一定还有另一个异于点 A的交点;
(3)当 c< a≤ c+3时,求出直线 y= kx+4与抛物线 y= ax 2﹣ bx+ c的另一个交点 B的坐标;记抛物线顶点为 M,抛物线对称轴与直线 y= kx+4的交点为 N,设 S= S △ AMN﹣ S △ BMN,写出 S关于 a的函数,并判断 S是否有最大值?如果有,求出最大值;如果没有,请说明理由.
已知:如图,点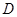 在
在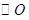 的直径
的直径 的延长线上,点
的延长线上,点 在
在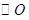 上,且
上,且 ,∠
,∠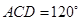 .
.
(1)求证: 是
是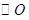 的切线;
的切线;
(2)若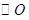 的半径为2,求图中阴影部分的面积.
的半径为2,求图中阴影部分的面积.
(1)如图①,用尺规作图作出圆的一条直径EF(不写作法,保留作图痕迹);
(2)如图②,A、B、C、D为圆上四点,AB∥CD,AB<CD,请只用无刻度的直尺,画出圆的一条直径EF(不写画法,保留画图痕迹).
如图,在Rt△ABC中,∠B=90°,AB=3cm,BC=4cm.点P从点A出发,以1cm/s的速度沿AB运动;同时,点Q从点B出发,以2cm/s的速度沿BC运动.当点Q到达点C时,P、Q两点同时停止运动.
(1)试写出△PBQ的面积S(cm2)与动点运动时间t(s)之间的函数表达式;
(2)运动时间t为何值时,△PBQ的面积最大?最大值是多少?
已知函数 (
( 为常数).
为常数).
(1)证明:无论m取何值,该函数与 轴总有两个交点;
轴总有两个交点;
(2)设函数的两交点的横坐标分别为 和
和 ,且
,且 ,求此函数的解析式.
,求此函数的解析式.
某旅行社为了吸引游客组团去旅游,推出了如下收费标准:
(1)若A单位组织该单位25名员工去旅游,需支付给该旅行社旅游费用_____元。
(2)若B单位共支付给该旅行社旅游费用27000元,请问B单位共有多少名员工去旅游?