设O为坐标原点,动点M在椭圆 上,过M作x轴的垂线,垂足为N,点P满足 .
(1)求点P的轨迹方程;
(2)设点Q在直线 上,且 .证明:过点P且垂直于OQ的直线l过C的左焦点F.
在对人们饮食习惯的一次调查中,共调查了124人,其中六十岁以上的70人,六十岁以下的54人,六十岁以上的人中有43人的饮食以蔬菜为主,另外27人则以肉类为主;六十岁以下的人中有21人饮食以蔬菜为主,另外33人则以肉类为主.(1)根据以上数据建立一个2×2的列联表;(2)判断人的饮食习惯是否与年龄有关,并做简要分析.
在一个数据组中,已知 是
是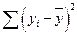 的两倍,
的两倍, 是
是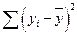 的
的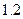 倍,试求这组数据的相关系数
倍,试求这组数据的相关系数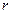 .(精确到
.(精确到 )
)
某化工厂为预测某产品的回收率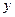 ,需要研究它和原料有效成分含量
,需要研究它和原料有效成分含量 之间的相关关系,现取
之间的相关关系,现取 对观测值,计算得
对观测值,计算得 ,求
,求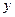 与
与 之间的回归直线方程.(精确到
之间的回归直线方程.(精确到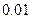 )
)
设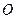 为坐标原点,
为坐标原点, 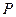 为直线
为直线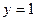 上动点,
上动点, 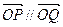 ,
,  , 求
, 求 点的轨迹方程.
点的轨迹方程.
已知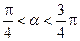 ,
, 且
且 ,
, ,求
,求 的值.
的值.