设函数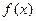 满足:
满足: (其中a、b、c均为常数,且|a|≠|b|),试求
(其中a、b、c均为常数,且|a|≠|b|),试求 .
.
(本小题12分)如图7,已知圆 ,设A为圆C与x轴负半轴的交点,过点A作圆C的弦AM,并使弦AM的中点恰好落在y轴上.
,设A为圆C与x轴负半轴的交点,过点A作圆C的弦AM,并使弦AM的中点恰好落在y轴上.
(1)当 在
在 内变化时,求点M的轨迹E的方程;
内变化时,求点M的轨迹E的方程;
(2)已知定点P(-1,1)和Q(1,0),设直线PM、QM与轨迹E的另一个交点分别是M1、M2 . 求证:当M点在轨迹E上变动时,只要M1、M2都存在且M1 M2,则直线M1M2恒过一个定点,并求出这个定点。
M2,则直线M1M2恒过一个定点,并求出这个定点。
(本小题12分)已知椭圆C的中心在坐标原点O,焦点在x轴上,离心率等于 ,
,
它的一个顶点B恰好是抛物线 的焦点。
的焦点。
(1)求椭圆C的方程;
(2)直线 与椭圆C交于
与椭圆C交于 两点,那么椭圆C的右焦点
两点,那么椭圆C的右焦点 是否可以成为
是否可以成为 的垂心?若可以,求出直线
的垂心?若可以,求出直线 的方程;若不可以,请说明理由.(注: 垂心是三角形三条高线的交点)
的方程;若不可以,请说明理由.(注: 垂心是三角形三条高线的交点)
(本小题12分) 如图,在边长为12的正方形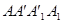 中,点B、C在线段AA′上,且AB=3,BC=4.作BB1∥AA1,分别交A1A1′、AA1′于点B1、P;作CC1∥AA1,分别交A1A1′、AA1′于点C1、Q. 现将该正方形沿BB1,CC1折叠,使得
中,点B、C在线段AA′上,且AB=3,BC=4.作BB1∥AA1,分别交A1A1′、AA1′于点B1、P;作CC1∥AA1,分别交A1A1′、AA1′于点C1、Q. 现将该正方形沿BB1,CC1折叠,使得 与AA1重合,构成如图(2)所示的三棱柱ABC-A1B1C1.
与AA1重合,构成如图(2)所示的三棱柱ABC-A1B1C1.
(1)在三棱柱ABC-A1B1C1中,求证:AP⊥BC;
(2)在三棱柱ABC-A1B1C1中,连接AQ与A1P,求四面体AA1QP的体积;
(3)在三棱柱ABC- A1B1C1中,求直线 PQ与直线AC所成角的余弦值.
(本小题13分)如图,在直三棱柱ABC-A1B1C1中, ,点E、F、G分别是AA1、
,点E、F、G分别是AA1、
AC、BB1的中点,且CG⊥C1G .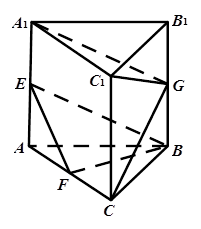
(1)求证:CG//面BEF;
(2)求证:面BEF⊥面A1C1G .
(本小题13分)已知命题A:方程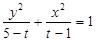 表示焦点在
表示焦点在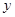 轴上的椭圆;
轴上的椭圆;
命题B:实数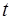 使得不等式
使得不等式 成立。
成立。
(1)若命题A为真,求实数 的取值范围;
的取值范围;
(2)若命题B是命题A的必要不充分条件,求实数 的取值范围。
的取值范围。