某商场预计2009年1月份起前x个月,顾客对某种商品的需求总量p(x)(单位:件)与x的关系近似地满足p(x)=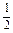 x(x+1)(39-2x),(x∈N*,且x≤12).该商品第x月的进货单价q(x)(单位:元)与x的近似关系是q(x)=150+2x.(x∈N*,且x≤12).(1)写出今年第x月的需求量f(x)件与x的函数关系式;(2)该商品每件的售价为185元,若不计其他费用且每月都能满足市场需求,试问商场2009年第几月份销售该商品的月利润最大,最大月利润为多少元?
x(x+1)(39-2x),(x∈N*,且x≤12).该商品第x月的进货单价q(x)(单位:元)与x的近似关系是q(x)=150+2x.(x∈N*,且x≤12).(1)写出今年第x月的需求量f(x)件与x的函数关系式;(2)该商品每件的售价为185元,若不计其他费用且每月都能满足市场需求,试问商场2009年第几月份销售该商品的月利润最大,最大月利润为多少元?
(本题满分15分)函数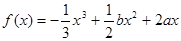 ,
,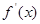 是它的导函数.
是它的导函数.
(Ⅰ)当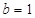 时,若
时,若 在区间
在区间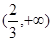 存在单调递增区间,求
存在单调递增区间,求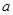 的取值范围。
的取值范围。
(Ⅱ)当 时,
时,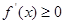 恒成立,求
恒成立,求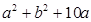 的最小值.
的最小值.
(本题满分14分)四棱锥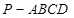 的底面
的底面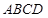 是直角梯形,
是直角梯形,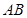 ∥
∥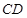 ,
,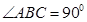 ,
, ,
,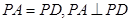 ,
,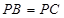
(Ⅰ)求证:平面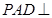 平面
平面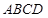 ;
;
(Ⅱ)求直线 与平面
与平面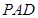 所成角的正切值.
所成角的正切值.
(本题满分14分)设等比数列 的首项为
的首项为 ,公比
,公比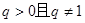 ,前
,前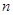 项和为
项和为
(Ⅰ)当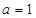 时,
时, 三数成等差数列,求数列
三数成等差数列,求数列 的通项公式;
的通项公式;
(Ⅱ)对任意正整数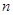 ,命题甲:
,命题甲: 三数构成等差数列.
三数构成等差数列.
命题乙: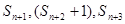 三数构成等差数列.
三数构成等差数列.
求证:对于同一个正整数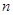 ,命题甲与命题乙不能同时为真命题.
,命题甲与命题乙不能同时为真命题.
(本题满分14分)设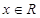 ,向量
,向量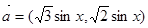 ,
,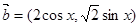 ,函数
,函数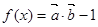 .(Ⅰ)在区间
.(Ⅰ)在区间 内,求
内,求 的单调递减区间;
的单调递减区间;
(Ⅱ)若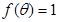 ,其中
,其中 ,求
,求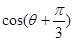 .
.
设 x1、x2(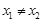 )是函数
)是函数  (
( )的两个极值点.(I)若
)的两个极值点.(I)若 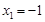 ,
,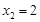 ,求函数
,求函数  的解析式;
的解析式;
(II)若 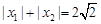 ,求 b 的最大值;
,求 b 的最大值;
(III)设函数 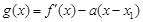 ,
,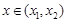 ,当
,当 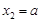 时,求
时,求 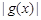 的最大值.
的最大值.