已知抛物线 ,顶点为 A,且经过点 ,点 .
(1)求抛物线的解析式;
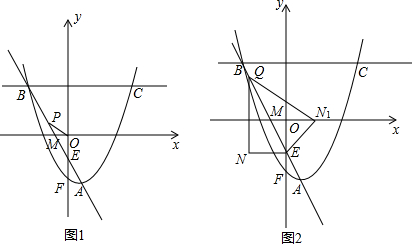
(2)如图1,直线 AB与 x轴相交于点 M, y轴相交于点 E,抛物线与 y轴相交于点 F,在直线 AB上有一点 P,若∠ OPM=∠ MAF,求△ POE的面积;
(3)如图2,点 Q是折线 A﹣ B﹣ C上一点,过点 Q作 QN∥ y轴,过点 E作 EN∥ x轴,直线 QN与直线 EN相交于点 N,连接 QE,将△ QEN沿 QE翻折得到△ QEN 1,若点 N 1落在 x轴上,请直接写出 Q点的坐标.
已知:抛物线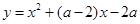 (
( 为常数,且
为常数,且 ).
).
(1)求证:抛物线与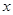 轴有两个交点;
轴有两个交点;
(2)设抛物线与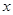 轴的两个交点分别为
轴的两个交点分别为 、
、 (
(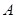 在
在 左侧),与
左侧),与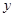 轴的交点为
轴的交点为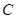 .
.
当 时,求抛物线的解析式;
时,求抛物线的解析式;
已知:如图,在Rt△ABC中,∠C=90°, D、E分别为AB、 AC边上的点,且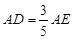 ,连结DE.若AC=3,AB=5,猜想DE与AB有怎样的位置关系?并证明你的结论.
,连结DE.若AC=3,AB=5,猜想DE与AB有怎样的位置关系?并证明你的结论.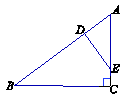
在△ABC中,∠A=90°,点D在线段BC上,∠EDB=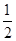 ∠C,BE⊥DE,垂足为E,DE与AB相交于点F.
∠C,BE⊥DE,垂足为E,DE与AB相交于点F.
(1)当AB=AC时,(如图1),
①∠EBF=_______°;
②探究线段BE与FD的数量关系,并加以证明;
(2)当AB=kAC时(如图2),求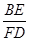 的值(用含k的式子表示).
的值(用含k的式子表示).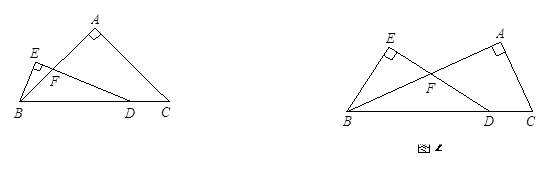
为了预防流感,某校在休息天用药熏消毒法对教室进行消毒.已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比,药物释放完毕后,y与t的函数关系式为y=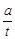 (a为常数),如图所示,根据图中提供的信息,解答下面的问题:
(a为常数),如图所示,根据图中提供的信息,解答下面的问题:
(1)写出从药物释放开始,y与t之间的两个函数关系式及相应的自变量的取值范围;
(2)据测定,当空气中每立方米的含药量降低到0.25毫克以下时,学生方可进入教室,那么从药物释放开始,至少需要经过多少小时后,学生才能进入教室?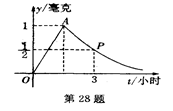
“五一”期间,为了满足广大人民的消费需求,某商店计划用160 000元购进一批家电,这批家电的进价和售价如下表:
(1)若全部资金用来购买彩电和洗衣机共100台,则商家可以购买彩电和洗衣机各多少台?
(2)若在现有资金160 000元允许的范围内,购买上表中三类家电共100台,其中彩电台数和冰箱台数相同,且购买洗衣机的台数不超过购买彩电的台数,请你算一算,共有几种进货方案?哪种进货方案能使商店销售完这批家电后获得的利润最大?并求出最大利润.(利润=售价-进价)