已知Rt△ OAB,∠ OAB=90°,∠ ABO=30°,斜边 OB=4,将Rt△ OAB绕点 O顺时针旋转60°,如图1,连接 BC.
(1)填空:∠ OBC= °;
(2)如图1,连接 AC,作 OP⊥ AC,垂足为 P,求 OP的长度;
(3)如图2,点 M, N同时从点 O出发,在△ OCB边上运动, M沿 O→ C→ B路径匀速运动, N沿 O→ B→ C路径匀速运动,当两点相遇时运动停止,已知点 M的运动速度为1.5单位/秒,点 N的运动速度为1单位/秒,设运动时间为 x秒,△ OMN的面积为 y,求当 x为何值时 y取得最大值?最大值为多少?

已知 ,求代数式
,求代数式 的值.
的值.
(1) ;
;
(2) ;
;
(3) .
.
抛物线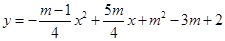 与x轴的交点分别为原点O和点A,点B(2,n)在这条抛物线上.
与x轴的交点分别为原点O和点A,点B(2,n)在这条抛物线上.
(1)求点B的坐标;
(2)点P在线段OA上,从点O出发向点A运动,过点P作x轴的垂线,与直线OB交于点E,以PE为边在PE右侧作正方形PEDC(当点P运动时,点C、D也随之运动).
①当正方形PEDC顶点D落在此抛物线上时,求OP的长;
②若点P从点O出发向点A作匀速运动,速度为每秒1个单位,同时线段OA上另一个点Q从点A出发向点O作匀速运动,速度为每秒2个单位(当点Q到达点O时停止运动,点P也停止运动).过Q作x轴的垂线,与直线AB交于点F,在QF的左侧作正方形QFMN(当点Q运动时,点M、N也随之运动).若点P运动到t秒时,两个正方形分别有一条边恰好落在同一条直线上,求此刻t的值.
某厂销售一种专利产品,现准备从专卖店销售和电视直销两种销售方案中选择一种进行销售.若只是专卖店销售,销售价格y(元/件)与月销量x(件)的函数关系式为y = x+150,成本为40元/件,无论销售多少,每月还需支出房租费52500元,设月利润为w专(元)(利润=销售额-成本-广告费).若只是电视直销,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为常数,40≤a≤80),当月销量为x(件)时,每月还需缴纳
x+150,成本为40元/件,无论销售多少,每月还需支出房租费52500元,设月利润为w专(元)(利润=销售额-成本-广告费).若只是电视直销,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为常数,40≤a≤80),当月销量为x(件)时,每月还需缴纳 x2元的广告费,设月利润为w电(元)(利润=销售额-成本-附加费).
x2元的广告费,设月利润为w电(元)(利润=销售额-成本-附加费).
(1)当x=1000时,y=元/件,w内=元;
(2)分别求出w专、w电与x间的函数关系式(不必写x的取值范围);
(3)当x为何值时,在专卖店销售的月利润最大?若是电视直销月利润的最大值与在专卖店销售月利润的最大值相同,求a的值;
(4)如果某月要将5000件产品全部销售完,请你通过分析帮公司决策,选择在专卖店还是电视直销才能使所获月利润较大?
已知一次函数y1=ax+b的图象与反比例函数y2= 的图象相交于A、B两点,坐标分别为(—2,4)、(4,—2)。
的图象相交于A、B两点,坐标分别为(—2,4)、(4,—2)。
(1)求两个函数的解析式;
(2)求△AOB的面积;
(3)直线AB上是否存在一点P(A除外),使△ABO与以B﹑P、O为顶点的三角形相似?若存在,直接写出顶点P的坐标。