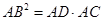在一次数学兴趣小组活动中,李燕和刘凯两位同学设计了如图所示的两个转盘做游戏(每个转盘被分成面积相等的几个扇形,并在每个扇形区域内标上数字).游戏规则如下:两人分别同时转动甲、乙转盘,转盘停止后,若指针所指区域内两数和小于12,则李燕获胜;若指针所指区域内两数和等于12,则为平局;若指针所指区域内两数和大于12,则刘凯获胜(若指针停在等分线上,重转一次,直到指针指向某一份内为止).
(1)请用列表或画树状图的方法表示出上述游戏中两数和的所有可能的结果;
(2)分别求出李燕和刘凯获胜的概率.

已知,如图,反比例函数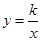 的图像与一次函数
的图像与一次函数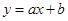 的图像相交于点
的图像相交于点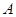
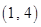 、
、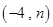 ,
,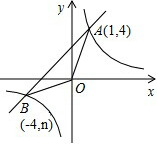
(1)试确定这两个函数的表达式;
(2)求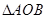 的面积;
的面积;
(3)直接写出使反比例函数的值大于一次函数的值的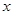 的取值范围.
的取值范围.
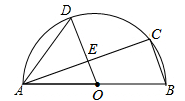
如图,已知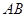 是半圆
是半圆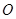 的直径,
的直径,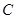 、
、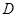 是半圆上的两点,且
是半圆上的两点,且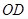 ∥
∥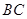 ,
,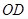 交
交 于点
于点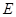 。
。
(1)若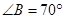 ,求
,求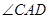 的度数;
的度数;
(2)若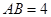 ,
,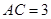 ,求
,求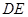 的长。
的长。
如图,在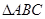 中,
中,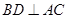 ,
, ,
,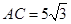 ,
,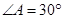
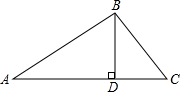
(1)求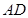 和
和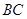 ;
;
(2)求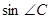
你喜欢转盘游戏吗?如图,图中的两个转盘分别被均匀地分成5个和4个扇形,每个扇形上都标有数字,同时自由转动两个转盘,转盘停止后,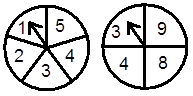
(1)请用列表法或树形图分析指针都落在奇数上的概率是多少?
(2)甲、乙两人约定:若转到的数字点数之和为奇数,则甲胜;反之,则乙胜.你认为这个游戏是否公平?说明你的理由.
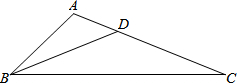
如图,已知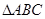 中,点
中,点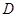 在
在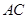 上,且
上,且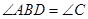 ,求证:
,求证: