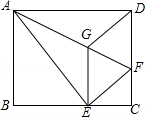
如图，将矩形ABCD沿AF折叠，使点D落在BC边上的点E处，过点E作 交AF于点G，连接DG．
（1）求证：四边形EFDG是菱形；
（2）探究线段EG、GF、AF之间的数量关系，并说明理由；
（3）若 ， ，求BE的长．
已知：
，
，以AB为一边作正方形ABCD，使P、D两点落在直线AB的两侧。
（1）如图，当∠APB=45°时，求AB及PD的长；
（2）当∠APB变化，且其它条件不变时，求PD 的最大值，及相应∠APB的大小。
如图，在直角坐标系中，O为坐标原点，二次函数
的图象与
轴的正半轴交于点
，与
轴的正半轴交交于点
，且
．设此二次函数图象的顶点为
。
（1）求这个二次函数的解析式；
（2）将
绕点顺时针旋转
后，点落到点
的位置．将上述二次函数图象沿轴向上或向下平移后经过点．请直接写出点的坐标和平移后所得图象的函数解析式；（3）设（2）中平移后所得二次函数图象与
轴的交点为
，顶点为
．点
在平移后的二次函数图象上，且满足
的面积是
面积的
倍，求点的坐标。
已知关于
的方程
有实根。（1）求
的值;（2）若关于
的方程
的所有根均为整数，求整数
的值。
如图①，△ABC，
，∠ABC=
，将△ABC绕点A顺时针旋转得△AB ¢C ¢，设旋转的角度是
。
（1）如图②，当
= °（用含的代数式表示）时，点B ¢恰好落在CA的延长线上；（2）如图③，连结BB ¢、CC ¢，CC ¢的延长线交斜边AB于点E，交BB ¢于点F．请写出图中两对相似三角形 ， 。
（不含全等三角形）。
已知：如图，在△ABC中，AB=AC= 5，BC= 8，D，E分别为BC，AB边上一点，∠ADE=∠C．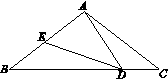
（1）求证：△BDE∽△CAD；
（2）若CD=2，求BE的长。