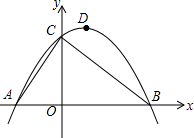
如图,已知点A的坐标为(﹣2,0),直线 与x轴、y轴分别交于点B和点C,连接AC,顶点为D的抛物线 过A、B、C三点.
(1)请直接写出B、C两点的坐标,抛物线的解析式及顶点D的坐标;
(2)设抛物线的对称轴DE交线段BC于点E,P是第一象限内抛物线上一点,过点P作x轴的垂线,交线段BC于点F,若四边形DEFP为平行四边形,求点P的坐标;
(3)设点M是线段BC上的一动点,过点M作 ,交AC于点N,点Q从点B出发,以每秒1个单位长度的速度沿线段BA向点A运动,运动时间为t(秒),当t(秒)为何值时,存在△QMN为等腰直角三角形?
一个动点在第一象限及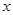 轴、
轴、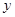 轴上运动,在第一秒钟,它从原点运动到
轴上运动,在第一秒钟,它从原点运动到 ,然后接着按图中箭头所示方向运动(即
,然后接着按图中箭头所示方向运动(即 ),且每秒移动一个单位,那么第100秒时动点所在位置的坐标是.
),且每秒移动一个单位,那么第100秒时动点所在位置的坐标是. 
已知:直线y=x+6交x轴于A点,交y轴于C两点,经过A和原点O的抛物线y==ax2+bx(a<0)的顶点B在直线AC上。
(1)求点A、C、B的坐标
(2)求出抛物线的函数关系式;
(3)以B点为圆心,以AB为半径作⊙B,将⊙B沿x轴翻折得到⊙D,试判断直线AC与⊙D的位置关系,并求出BD的长;
(4)若E为⊙B优弧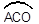 上一动点,连结AE、OE,问在抛物线上是否存在一点M,使∠MOA︰∠AEO=2︰3,若存在,试求出点M的坐标;若不存在,试说明理由
上一动点,连结AE、OE,问在抛物线上是否存在一点M,使∠MOA︰∠AEO=2︰3,若存在,试求出点M的坐标;若不存在,试说明理由
锐角△ABC中,BC=6, ,两动点M,N分别在边AB,AC上滑动,且MN∥BC,以MN为边向下作正方形MPQN,设其边长为x,正方形MPQN与△ABC公共部分的面积为y(y>0).
,两动点M,N分别在边AB,AC上滑动,且MN∥BC,以MN为边向下作正方形MPQN,设其边长为x,正方形MPQN与△ABC公共部分的面积为y(y>0).
(1) 求△ABC中边BC上高AD;
(2) 当 为何值时,PQ恰好落在边BC上(如图1);
为何值时,PQ恰好落在边BC上(如图1);
(3) 当PQ在 外部时(如图2),求y关于x的函数关系式(注明x的取值范围),并求出x为何值时y最大,最大值是多少?
外部时(如图2),求y关于x的函数关系式(注明x的取值范围),并求出x为何值时y最大,最大值是多少?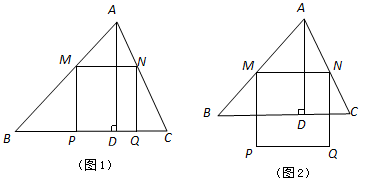
如图,以△ABC的边AB为直径的⊙O经过BC的中点D,过D作DE⊥AC于E。
(1)求证:AB=AC
(2)求证:DE是⊙O的切线
(3)若AB=10,∠ABC=300,求DE的长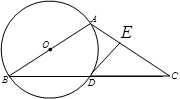
台湾“华航”客机失事后,祖国大陆海上搜救中心立即通知位于A、B两处的上海救捞人局所属专业救助轮“华意”轮、“沪救12”轮前往出事地点协助搜索。接到通知后,“华意”轮测得出事地点C在A的南偏东60°、“沪救12”轮测得出事地点C在B的南偏东30°。已知B在A的正东方向,且相距50海里,分别求出两艘船到达出事地点C的距离。