有一科技小组进行了机器人行走性能试验,在试验场地有 A、 B、 C三点顺次在同一笔直的赛道上,甲、乙两机器人分别从 A、 B两点同时同向出发,历时7分钟同时到达 C点,乙机器人始终以60米/分的速度行走,如图是甲、乙两机器人之间的距离 y(米)与他们的行走时间 x(分钟)之间的函数图象,请结合图象,回答下列问题:
(1) A、 B两点之间的距离是 米,甲机器人前2分钟的速度为 米/分;
(2)若前3分钟甲机器人的速度不变,求线段 EF所在直线的函数解析式;
(3)若线段 FG∥ x轴,则此段时间,甲机器人的速度为 米/分;
(4)求 A、 C两点之间的距离;
(5)若前3分钟甲机器人的速度不变,直接写出两机器人出发多长时间相距28米.

如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E.
(1)求证:CD为⊙O的切线;
(2)若BD的弦心距OF=1,∠ABD=30°,求图中阴影部分的面积.(结果保留π)
先化简,再求值: ,其中
,其中 ,
, .
.
(1)计算: ;
;
(2)解方程: .
.
如图,在梯形ABCD中,AD∥BC,∠B=90°,BC=6,AD=3,
∠DCB=30°.点E、F同时从B点出发,沿射线BC向右匀速移动.已知F点移动速度是E点移动速度的2倍,以EF为一边在CB的上方作等边△EFG.设E点移动距离为x(x>0).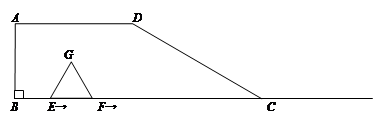
⑴△EFG的边长是___________ (用含有x的代数式表示),当x=2时,点G的位置在_______;
⑵若△EFG与梯形ABCD重叠部分面积是y,求
①当0<x≤2时,y与x之间的函数关系式;
②当2<x≤6时,y与x之间的函数关系式;
⑶探求⑵中得到的函数y在x取含何值时,存在最大值,并求出最大值.
如图,抛物线y=x2+bx+c与x轴交于A(-1,0)、B(3,0)两点,直线L与抛物线交于A、C两点,其中C点的横坐标为2.
(1)求抛物线的解析式及直线AC的解析式;
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值;
(3)点G是抛物线上的动点,在x轴上是否存在点F,使A、C、F、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由.