把三角形按如图所示的规律拼图案,其中第①个图案中有4个三角形,第②个图案中有6个三角形,第③个图案中有8个三角形, ,按此规律排列下去,则第⑦个图案中三角形的个数为
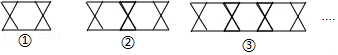
| A. |
12 |
B. |
14 |
C. |
16 |
D. |
18 |
为调查某大型企业员工对企业的满意程度,以下样本最具代表性的是
| A. |
企业男员工 |
| B. |
企业年满50岁及以上的员工 |
| C. |
用企业人员名册,随机抽取三分之一的员工 |
| D. |
企业新进员工 |
下列图形中一定是轴对称图形的是
| A. |
|
B. |
|
| C. |
|
D. |
|
2的相反数是
| A. |
|
B. |
|
C. |
|
D. |
2 |
若数 使关于 的不等式组 有且仅有四个整数解,且使关于 的分式方程 有非负数解,则所有满足条件的整数 的值之和是
| A. |
3 |
B. |
1 |
C. |
0 |
D. |
|