海静中学开展以"我最喜爱的职业"为主题的调查活动,围绕"在演员、教师、医生、律师、公务员共五类职业中,你最喜爱哪一类?(必选且只选一类)"的问题,在全校范围内随机抽取部分学生进行问卷调查,将调查结果整理后绘制成如图所示的不完整的统计图,请你根据图中提供的信息回答下列问题:
(1)本次调查共抽取了多少名学生?
(2)求在被调查的学生中,最喜爱教师职业的人数,并补全条形统计图;
(3)若海静中学共有1500名学生,请你估计该中学最喜爱律师职业的学生有多少名?

某地区共有1800名初三学生,为解决这些学生的体质健康状况,开学之初随机选取部分学生进行体育测试,以下是根据测试成绩绘制的统计图表的一部分.
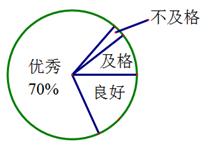
根据以上信息,解答下列问题:(1)本次测试学生体质健康成绩为良好的有_________人,达到优秀的人数占本次测试人数的百分比为____%.
本次测试学生人数为_________人,其中,体质健康成绩为及格的有________人,不及格的人数占本次测试总人数的百分比是__________%.
试估计该地区初三学生开学之初体质健康成绩达到良好及以上等级的学生数.
在□ABCD中,点E、F在AC上,且∠ABE=∠CDF,求证:BE=DF.
解方程
如图,抛物线y=ax2+bx+c经过A(1,0)、B(4,0)、C(0,3)三点.
(1)求抛物线的解析式;
(2)如图①,在抛物线的对称轴上是否存在点P,使得四边形PAOC的周长最小?若存在,求出四边形PAOC周长的最小值;若不存在,请说明理由.
(3)如图②,点Q是线段OB上一动点,连接BC,在线段BC上是否存在这样的点M,使△CQM为等腰三角形且△BQM为直角三角形?若存在,求点M的坐标;若不存在,请说明理由.
已知直线m∥n,点C是直线m上一点,点D是直线n上一点,CD与直线m、n不垂直,点P为线段CD的中点.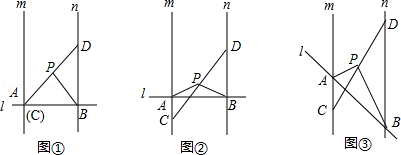
(1)操作发现:直线l⊥m,l⊥n,垂足分别为A、B,当点A与点C重合时(如图①所示),连接PB,请直接写出线段PA与PB的数量关系:.
(2)猜想证明:在图①的情况下,把直线l向上平移到如图②的位置,试问(1)中的PA与PB的关系式是否仍然成立?若成立,请证明;若不成立,请说明理由.
(3)延伸探究:在图②的情况下,把直线l绕点A旋转,使得∠APB=90°(如图③所示),若两平行线m、n之间的距离为2k.求证:PA•PB=k•AB.