已知:如图,在正方形 ABCD中,点 E在边 CD上, 于点 Q, 于点 P.
(1)求证: ;
(2)在不添加任何辅助线的情况下,请直接写出图中四对线段,使每对中较长线段与较短线段长度的差等于 PQ的长.

如图⑴所示的图形,像我们常见的学习用品——圆规。我们不妨把这样图形叫做“规形图”,那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?下面就请你发挥你的聪明才智,解决以下问题: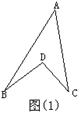
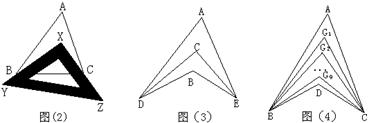
⑴观察“规形图”,试探究∠BDC与∠A、∠B、∠C之间的关系,并说明理由;
⑵请你直接利用以上结论,解决以下三个问题:
①如图(2),把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、XZ恰好经过点B、C,若∠A=50°,则∠ABX+∠ACX =__________°;
②如图(3),DC平分∠ADB, EC平分∠AEB,若∠DAE=50°,∠DBE=130°,求∠DCE的度数;
③如图(4),∠ABD,∠ACD的10等分线相交于点G1、G2 、G9,,若∠BDC=1400,∠BG1C=77°,求∠A的度数。
、G9,,若∠BDC=1400,∠BG1C=77°,求∠A的度数。
如图,是 的正方形网格(每个小正方形的边长为1),点A、B、C、D、E、F、G七点在各点上。
的正方形网格(每个小正方形的边长为1),点A、B、C、D、E、F、G七点在各点上。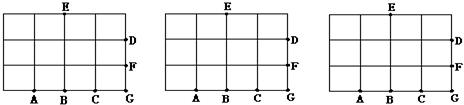
图⑴图⑵备用图
请解答下列各题:
⑴在图⑴中画一个面积为1的直角三角形(三角形的顶点从以上七个点中选择),并将你所画的三角形向左平移2个单位,向上平移1个单位(用阴影表示);
⑵在图⑵中画一个面积为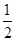 的钝角三角形(三角形的顶点从以上七个点中选择);
的钝角三角形(三角形的顶点从以上七个点中选择);
⑶在以上七点中选择三点作为三角形的顶点,其中面积为3的三角形有_____个。
如图,已知:CF⊥AB于F,ED⊥AB于D,∠1=∠2,说明:FG∥BC.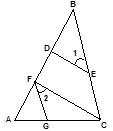
如图,已知△ABC.
(1)画中线CE;
(2)画高AD、BF、CG.
如图,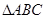 中,
中,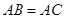 ,
, 是
是 上一点,
上一点, 是
是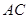 延长线上一点,
延长线上一点,
且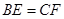 ,若
,若 与
与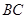 相交于
相交于 ,求证:
,求证: 。
。