如图,在平面直角坐标系中, O为坐标原点,抛物线 经过 A(﹣4,0), B(0,4)两点,与 x轴交于另一点 C,直线 与 x轴交于点 D,与 y轴交于点 E.
(1)求抛物线的解析式;
(2)点 P是第二象限抛物线上的一个动点,连接 EP,过点 E作 EP的垂线 l,在 l上截取线段 EF,使 EF= EP,且点 F在第一象限,过点 F作 轴于点 M,设点 P的横坐标为 t,线段 FM的长度为 d,求 d与 t之间的函数关系式(不要求写出自变量 t的取值范围);
(3)在(2)的条件下,过点 E作 交 MF的延长线于点 H,连接 DH,点 G为 DH的中点,当直线 PG经过 AC的中点 Q时,求点 F的坐标.

一位同学想利用树的影长测量树高,他在某一时刻测得长为1m的竹竿的影长为0.9m,但当他马上测量树的影长时,因树靠近一幢建筑物,影子不全落在地面上,有一部分影子落在墙上,如图,他先测得留在墙上的影子高CD为1.2m,又测得地面上的影子长BC为2.7m,则树高AB为多少?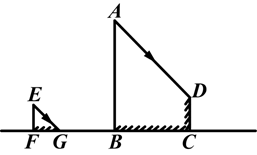
如图,在△ABC中,点D是AB的中点,点E在边AC上,且∠AED=∠ABC,如果AE=3,EC=1,求边AB的长.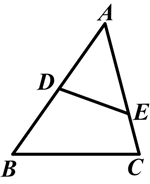
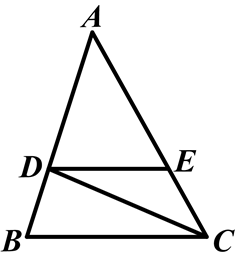
如图所示,在△ABC中,AB=4,探究以下问题:
(1)如图①所示,DE∥BC,DE把△ABC分成面积相等的两部分,即S1=S2,求AD的长;
(2)如图②所示,DE∥FG∥BC,DE,FG把△ABC分成面积相等的三部分,即S1=S2=S3,求AD的长;
(3)如图③所示,DE∥FG∥HK∥…∥BC,DE,FG,HK,…把△ABC分成面积相等的n部分,即S1=S2=S3=…=Sn,请直接写出AD的长.
如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位,当点P运动到C时,两点都停止,设运动时间为t秒.
(1)求线段CD的长.
(2)设△CPQ的面积为S,求S与t之间的函数关系式,并确定在运动过程中是否存在某一时刻t,使得S△CPQ︰S△ABC=9︰100?若存在,求出t的值;若不存在,说明理由.
(3)当t为何值时,△CPQ为等腰三角形?
如图所示,在△ABC中,DE∥BC,S△ADE︰S△ABC=4︰9,求:
(1)AE︰EC;
(2)S△ADE︰S△CDE.