已知二次函数
(1)当 时,求这个二次函数的顶点坐标;
(2)求证:关于x的一元二次方程
有两个不相等的实数根;
(3)如图,该二次函数与x轴交于A、B两点(A点在B点的左侧),与y轴交于C点,P是y轴负半轴上一点,且 ,直线AP交BC于点Q,求证: .

如图所示,在ΔABC中,∠A=800,∠B=300,CD平分∠ACB,DE∥AC。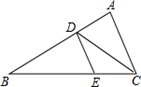
(1)求∠DEB的度数;(2)求∠EDC的度数。
如图是六个棱长为1的立方块组成一的一个几何体,画出它的三视图。
阅读题
先阅读理解,再回答下列问题:
因为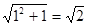 ,且
,且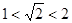 ,所以
,所以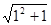 的整数部分为1;
的整数部分为1;
因为 ,且
,且 ,所以
,所以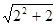 的整数部分为2;
的整数部分为2;
因为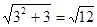 ,且
,且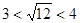 ,所以
,所以 的整数部分为3;
的整数部分为3;
以此类推,我们会发现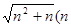 为正整数)的整数部分为______,请说明理由.
为正整数)的整数部分为______,请说明理由.
已知二次函数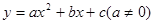 的图象以A(-1,4)为顶点,且过点B(2,0)
的图象以A(-1,4)为顶点,且过点B(2,0)
(1)求该函数的关系式;
(2)若将该函数图象以顶点为中心旋转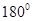 ,求旋转后抛物线的关系式.
,求旋转后抛物线的关系式.
设 是方程
是方程 的两个不相等的实数根,(1)求
的两个不相等的实数根,(1)求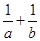 的值
的值
(2)求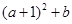 的值
的值