如图,在平面直角坐标系中,抛物线 交 轴于点 和 ,交 轴于点 ,抛物线的对称轴交 轴于点 ,交抛物线于点 .
(1)求抛物线的解析式;
(2)将线段 绕着点 沿顺时针方向旋转得到线段 ,旋转角为 ,连接 , ,求 的最小值;
(3) 为平面直角坐标系中一点,在抛物线上是否存在一点 ,使得以 , , , 为顶点的四边形为矩形?若存在,请写出点 的横坐标;若不存在,请说明理由.

某数学兴趣小组在数学课外活动中,对多边形内两条互相垂直的线段做了如下探究: 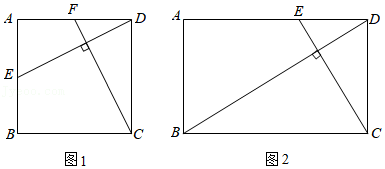
【观察与猜想】
(1)如图1,在正方形 中,点 , 分别是 , 上的两点,连接 , , ,则 的值为 ;
(2)如图2,在矩形 中, , ,点 是 上的一点,连接 , ,且 ,则 的值为 ;
【类比探究】
(3)如图3,在四边形 中, ,点 为 上一点,连接 ,过点 作 的垂线交 的延长线于点 ,交 的延长线于点 ,求证: ;

【拓展延伸】
(4)如图4,在 中, , , ,将 沿 翻折,点 落在点 处得 ,点 , 分别在边 , 上,连接 , , .
①求 的值;
②连接 ,若 ,写出 的长度.
如图, 是 的直径, 为 上一点 不与点 , 重合)连接 , ,过点 作 ,垂足为点 .将 沿 翻折,点 落在点 处得 , 交 于点 .
(1)求证: 是 的切线;
(2)若 , ,求阴影部分面积.

渠县是全国优质黄花主产地,某加工厂加工黄花的成本为30元 千克,根据市场调查发现,批发价定为48元 千克时,每天可销售500千克,为增大市场占有率,在保证盈利的情况下,工厂采取降价措施,批发价每千克降低1元,每天销量可增加50千克.
(1)写出工厂每天的利润 元与降价 元之间的函数关系.当降价2元时,工厂每天的利润为多少元?
(2)当降价多少元时,工厂每天的利润最大,最大为多少元?
(3)若工厂每天的利润要达到9750元,并让利于民,则定价应为多少元?
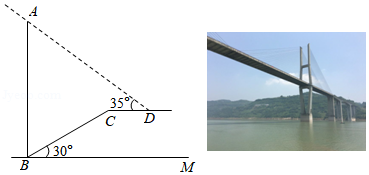
2021年,达州河边新建成了一座美丽的大桥.某学校数学兴趣小组组织了一次测桥墩高度的活动,如图,桥墩刚好在坡角为 的河床斜坡边,斜坡 长为48米,在点 处测得桥墩最高点 的仰角为 , 平行于水平线 , 长为 米,求桥墩 的高(结果保留1位小数). , , ,