如图,随着我市铁路建设进程的加快,现规划从 地到 地有一条笔直的铁路通过,但在附近的 处有一大型油库,现测得油库 在 地的北偏东 方向上,在 地的西北方向上, 的距离为 米.已知在以油库 为中心,半径为200米的范围内施工均会对油库的安全造成影响.问若在此路段修建铁路,油库 是否会受到影响?请说明理由.
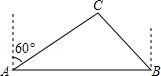
如图:在△ABC中,AD⊥BC,垂足是D.
(1)作△ABC的外接圆O,作直径AE(尺规作图);
(2)若AB=8,AC=6,AD=5,求△ABC的外接圆直径AE的长.
如图,P是正方形内一点,将△ABP绕点B顺时针方向旋转能与△CBP′重合,若BP=3,求PP′.
解方程:3x(x+5)=x+5
如图,平行四边形ABCD在平面直角坐标系中,点A的坐标为(-2,0),点B的坐标为(0,4),抛物线 经过点A和C.
经过点A和C.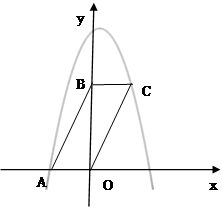
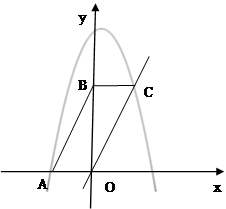
(1)求抛物线的解析式.
(2)该抛物线的对称轴将平行四边形ABCO分成两部分,对称轴左侧部分的图形面积记为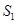 ,右侧部分图形的面积记为
,右侧部分图形的面积记为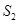 ,求
,求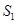 与
与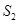 的比.
的比.
(3)在y轴上取一点D,坐标是(0,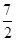 ),将直线OC沿x轴平移到
),将直线OC沿x轴平移到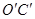 ,点D关于直线
,点D关于直线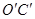 的对称点记为
的对称点记为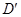 ,当点
,当点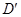 正好在抛物线上时,求出此时点
正好在抛物线上时,求出此时点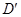 坐标并直接写出直线
坐标并直接写出直线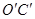 的函数解析式.
的函数解析式.
长岭中心中学九年级数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销量的相关信息如下表:
| 时间x(天) |
1≤x<50 |
50≤x≤90 |
| 售价(元/件) |
x+40 |
90 |
| 每天销量(件) |
200﹣2x |
已知该商品的进价为每件30元,设销售该商品的每天利润为y元.
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.