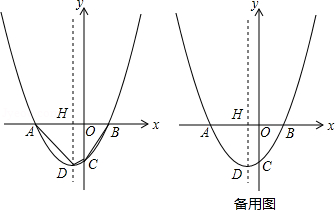
如图，在平面直角坐标系 中，抛物线 与 轴交于 ， 两点（点 在点 的左侧），与 轴交于点 ，顶点为 ，对称轴与 轴交于点 ，过点 的直线 交抛物线于 ， 两点，点 在 轴的右侧．
（1）求 的值及点 ， 的坐标；
（2）当直线 将四边形 分为面积比为 的两部分时，求直线 的函数表达式；
（3）当点 位于第二象限时，设 的中点为 ，点 在抛物线上，则以 为对角线的四边形 能否为菱形？若能，求出点 的坐标；若不能，请说明理由．
计算：
（1）、
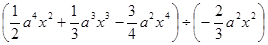
（2）、（ab+1）2－（ab－1）2
（3）、20122+20132-4024×2013
（4）、（1－y）2（1+y）2（1+y2）2
（5）、化简求值：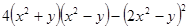
，其中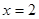
，
。
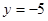如图，OB，OC是∠AOD的任意两条射线，OM平分∠AOB，ON平分∠COD，若∠MON=70°，∠BOC=30°，求∠AOD的度数。
如图已知点C为AB上一点，AC＝12cm，CB＝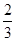
AC，D、E分别为AC、AB的中点，求DE的长。
如图，在公路l的两旁有两个工厂A、B，要在公路上搭建一个货场让A、B两厂使用，要使货场到A、B两厂的距离之和最小，问货场应建在什么位置？为什么？
把一边长为40cm的正方形硬纸板，进行适当的剪裁，折成一个长方形盒子（纸板的厚度忽略不计）。
（1）如图1，若在正方形硬纸板的四角各剪一个同样大小的正方形，将剩余部分折成一个无盖的长方形盒子。
①要使折成的长方形盒子的底面积为484cm2，那么剪掉的正方形的边长为多少？
②折成的长方形盒子的侧面积是否有最大值？如果有，求出这个最大值及此时剪掉的正方形的边长；如果没有，请说明理由。
（2）如图2在正方形硬纸板上剪掉一些矩形（图2中阴影为剪去部分），将剩余部分折成一个有盖的长方形盒子，若折成的一个长方形盒子的表面积为550cm2，求此时长方形盒子的长、宽、高。