如图,在 中, , 的平分线交 于点 , ,以点 为圆心 为半径作半圆.
(1)求证: 为 的切线;
(2)如果 ,求 的值.

(年湖北武汉10分)如图,Rt△ABC中,∠ACB=90°,AC=6 cm,BC=8 cm,动点P从点B出发,在BA边上以每秒5 cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4 cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.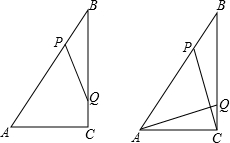
(1)若△BPQ与△ABC相似,求t的值;
(2)连接AQ、CP,若AQ⊥CP,求t的值;
(3)试证明:PQ的中点在△ABC的一条中位线上.
(年贵州安顺12分)如图,已知AB是⊙O的直径,BC是⊙O的弦,弦ED⊥AB于点F,交BC于点G,过点C的直线与ED的延长线交于点P,PC=PG.
(1)求证:PC是⊙O的切线;
(2)当点C在劣弧AD上运动时,其他条件不变,若BG2=BF•BO.求证:点G是BC的中点;
(3)在满足(2)的条件下,AB=10,ED= ,求BG的长.
,求BG的长.
(年贵州安顺12分)如图,已知AB是⊙O的直径,BC是⊙O的弦,弦ED⊥AB于点F,交BC于点G,过点C的直线与ED的延长线交于点P,PC=PG.
(1)求证:PC是⊙O的切线;
(2)当点C在劣弧AD上运动时,其他条件不变,若BG2=BF•BO.求证:点G是BC的中点;
(3)在满足(2)的条件下,AB=10,ED=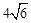 ,求BG的长.
,求BG的长.
(年广西玉林、防城港10分)如图,在正方形ABCD中,点M是BC边上的任一点,连接AM并将线段AM绕M顺时针旋转90°得到线段MN,在CD边上取点P使CP=BM,连接NP,BP.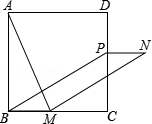
(1)求证:四边形BMNP是平行四边形;
(2)线段MN与CD交于点Q,连接AQ,若△MCQ∽△AMQ,则BM与MC存在怎样的数量关系?请说明理由.
(年广西河池10分)⊙O的半径为5,AB是⊙O的直径,点C在⊙O上,点D在直线AB上.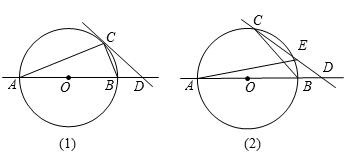
(1)如图(1),已知∠BCD=∠BAC,求证:CD是⊙O的切线;
(2)如图(2),CD与⊙O交于另一点E,BD:DE:EC=2;3:5求圆心O到直线CD的距离;
(3)若图(2)中的点D是直线AB上的动点,点D在运动过程中,会出现在C,D,E三点中,其中一点是另两点连线的中点的情况,问这样的情况出现几次?