我们规定：若m⃗(a,b)，n⃗(c,d)，则m⃗·n⃗ac-优题课

题文

我们规定：若 $\vec{m} = (a, b)$ ， $\vec{n} = (c, d)$ ，则 $\vec{m} \cdot \vec{n} = ac + bd$ ．如 $\vec{m} = (1, 2)$ ， $\vec{n} = (3, 5)$ ，则 $\vec{m} \cdot \vec{n} = 1 \times 3 + 2 \times 5 = 13$ ．

（1）已知 $\vec{m} = (2, 4)$ ， $\vec{n} = (2, - 3)$ ，求 $\vec{m} \cdot \vec{n}$ ；

（2）已知 $\vec{m} = (x - a, 1)$ ， $\vec{n} = (x - a, x + 1)$ ，求 $y = \vec{m} \cdot \vec{n}$ ，问 $y = \vec{m} \cdot \vec{n}$ 的函数图象与一次函数 $y = x - 1$ 的图象是否相交，请说明理由．

科目数学题型解答题难度中等

知识点：根的判别式

登录免费查看答案和解析

相关试题

(本小题满分10分)如图，已知点A（-1，m）与B（2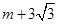，）是反比例函数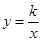图象上的两个点．（1）求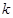的值；（2）若C点坐标为（-1，0），则在反比例函数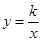图像上是否存在点D，使得以A、B、C、D为顶点的四边形为梯形？若存在，求D点的坐标，若不存在说明理由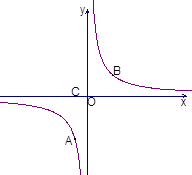

（本小题10分）如图，在正方形网格图中建立一直角坐标系，一条圆弧经过网格点A（0，2），B（4，2）C（6，0），解答下列问题：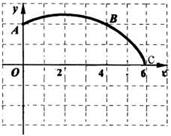

（1）请在图中确定该圆弧所在圆心D点的位置，则D点坐标为________ ；
（2）连结AD，CD，求⊙D的半径（结果保留根号）；
（3）求扇形DAC的面积. （结果保留π）

（本小题8分）某商店购进一批冬季保暖内衣，每套进价为100元，售价为130元，每星期可卖出80套．商家决定降价促销，根据市场调查，每降价5元，每星期可多卖出20套．

（1）求商家降价前每星期的销售利润为多少元？
（2）降价后，商家要使每星期的销售利润最大，应该售价定为多少元？最大销售利润是多少？

（本小题6分）如图，MN为半圆O的直径，半径OA⊥MN, D为OA的中点，过点D作BC//MN，

求证：( 1 ) 四边形ABOC为菱形； (2)∠MNB=∠BAC

（本小题6分）
已知一抛物线与x轴的交点是、B（1，0），且经过点C（2，8）。
（1）求该抛物线的解析式；　　　　
（2）求该抛物线的顶点坐标。

试卷网试题网古诗词网作文网范文网