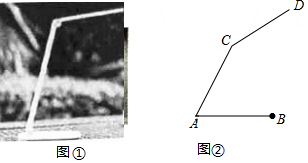
图①是放置在水平面上的台灯,图②是其侧面示意图(台灯底座高度忽略不计),其中灯臂 ,灯罩 ,灯臂与底座构成的 . 可以绕点 上下调节一定的角度.使用发现:当 与水平线所成的角为 时,台灯光线最佳.现测得点 到桌面的距离为 .请通过计算说明此时台灯光线是否为最佳?(参考数据: 取 .
某楼盘准备以每平方米6000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,房地产开发商为了加快资金周转,对价格经过两次下调后,决定以每平方米4860元的均价开盘销售。
(1)求平均每次下调的百分率;
(2)某人准备以开盘价均价购买一套100平方米的住房,开发商给予以下两种优惠方案以供选择:①打9.8折销售;②不打折,一次性送装修费每平方米80元,试问哪种方案更优惠?
(1)一个人由山底爬到山顶,需先爬450的山坡200m,再爬300的山坡300m,求山的高度(结果可保留根号)。
(2)如图,△ABC与△ABD中, AD与BC相交于O点,∠1=∠2,请你添加一个条件(不再添加其它线段,不再标注或使用其他字母),使AC=BD,并给出证明.你添加的条件是: 。
证明:
如图,直线 与坐标轴分别交于点A、B,与直线y=x交于点C.在线段OA上,动点Q以每秒1个单位长度的速度从点O出发向点A做匀速运动,同时动点P从点A出发向点O做匀速运动,当点P、Q其中一点停止运动时,另一点也停止运动.分别过点P、Q作x轴的垂线,交直线AB、OC于点E、F,连接EF.若运动时间为t秒,在运动过程中四边形PEFQ总为矩形(点P、Q重合除外).
与坐标轴分别交于点A、B,与直线y=x交于点C.在线段OA上,动点Q以每秒1个单位长度的速度从点O出发向点A做匀速运动,同时动点P从点A出发向点O做匀速运动,当点P、Q其中一点停止运动时,另一点也停止运动.分别过点P、Q作x轴的垂线,交直线AB、OC于点E、F,连接EF.若运动时间为t秒,在运动过程中四边形PEFQ总为矩形(点P、Q重合除外).
(1)求点P运动的速度是多少?
(2)当t为多少秒时,矩形PEFQ为正方形?
(3)当t为多少秒时,矩形PEFQ的面积S最大?并求出最大值.
如图1,在平面直角坐标系中,O为坐标原点,P是反比例函数 (x>0)图象上任意一点,以P为圆心,PO为半径的圆与坐标轴分别交于点A、B.
(x>0)图象上任意一点,以P为圆心,PO为半径的圆与坐标轴分别交于点A、B.
(1)求证:线段AB为⊙P的直径;
(2)求△AOB的面积;
(3)如图2,Q是反比例函数 (x>0)图象上异于点P的另一点,以Q为圆心,QO为半径画圆与坐标轴分别交于点C、D.
(x>0)图象上异于点P的另一点,以Q为圆心,QO为半径画圆与坐标轴分别交于点C、D.
求证:DO•OC=BO•OA.
阅读材料:若a,b都是非负实数,则 .当且仅当a=b时,“=”成立.
.当且仅当a=b时,“=”成立.
证明:∵ ,∴
,∴ .
.
∴ .当且仅当a=b时,“=”成立.
.当且仅当a=b时,“=”成立.
举例应用:已知x>0,求函数 的最小值.
的最小值.
解: .当且仅当
.当且仅当 ,即x=1时,“=”成立.
,即x=1时,“=”成立.
当x=1时,函数取得最小值,y最小=4.
问题解决:汽车的经济时速是指汽车最省油的行驶速度.某种汽车在每小时70~110公里之间行驶时(含70公里和110公里),每公里耗油 升.若该汽车以每小时x公里的速度匀速行驶,1小时的耗油量为y升.
升.若该汽车以每小时x公里的速度匀速行驶,1小时的耗油量为y升.
(1)求y关于x的函数关系式(写出自变量x的取值范围);
(2)求该汽车的经济时速及经济时速的百公里耗油量(结果保留小数点后一位).