如图，抛物线yax2bx4交x轴于A(−3,0)，B(4,0-优题课

题文

如图，抛物线 $y = a x^{2} + bx + 4$ 交 $x$ 轴于 $A (- 3, 0)$ ， $B (4, 0)$ 两点，与 $y$ 轴交于点 $C$ ，连接 $AC$ ， $BC$ ．点 $P$ 是第一象限内抛物线上的一个动点，点 $P$ 的横坐标为 $m$ ．

（1）求此抛物线的表达式；

（2）过点 $P$ 作 $PM ⊥ x$ 轴，垂足为点 $M$ ， $PM$ 交 $BC$ 于点 $Q$ ．试探究点 $P$ 在运动过程中，是否存在这样的点 $Q$ ，使得以 $A$ ， $C$ ， $Q$ 为顶点的三角形是等腰三角形．若存在，请求出此时点 $Q$ 的坐标，若不存在，请说明理由；

（3）过点 $P$ 作 $PN ⊥ BC$ ，垂足为点 $N$ ．请用含 $m$ 的代数式表示线段 $PN$ 的长，并求出当 $m$ 为何值时 $PN$ 有最大值，最大值是多少？

科目数学题型解答题难度较难

知识点：二次函数的性质待定系数法求二次函数解析式二次函数综合题

登录免费查看答案和解析

相关试题

（内蒙古呼和浩特）某玉米种子的价格为a元/千克，如果一次购买2千克以上的种子，超过2千克部分的种子价格打8折．某科技人员对付款金额和购买量这两个变量的对应关系用列表法做了分析，并绘制出了函数图象．以下是该科技人员绘制的图象和表格的不完整资料，已知点A的坐标为（2，10）．请你结合表格和图象：
（1）指出付款金额和购买量哪个变量是函数的自变量x，并写出表中a、b的值；
（2）求出当x＞2时，y关于x的函数解析式；
（2）甲农户将8．8元钱全部用于购买该玉米种子，乙农户购买了4165克该玉米种子，分别计算他们的购买量和付款金额．

（黔西南州）某地为了鼓励居民节约用水，决定实行两级收费制，即每月用水量不超过12吨（含12吨）时，每吨按政府补贴优惠价收费；每月超过12吨，超过部分每吨按市场调节价收费，小黄家1月份用水24吨，交水费42元．2月份用水20吨，交水费32元．
（1）求每吨水的政府补贴优惠价和市场调节价分别是多少元；
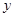（2）设每月用水量为吨，应交水费为元，写出与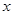之间的函数关系式；
（3）小黄家3月份用水26吨，他家应交水费多少元？

（贵州省安顺市）（本题10分）
如图，在平面直角坐标系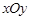中，一次函数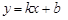的图象与反比例函数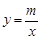的图象交于A（2，3）B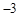（，n）两点．
（1）求一次函数和反比例函数的解析式；
（2）若P是轴上一点，且满足△PAB的面积是5，直接写出OP的长．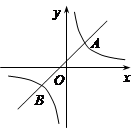

（贵州六盘水）（本小题10分）联通公司手机话费收费有A套餐（月租费15元，通话费每分钟0．1元）和B套餐（月租
费0元，通话费每分钟0．15元）两种。设A套餐每月话费为y₁（元），B套餐每月话费为y₂（元），月通话时间为x分钟．
（1）分别表示出y₁与x，y₂与x的函数关系式．
（2）月通话时间为多长时，A、B两种套餐收费一样？
（3）什么情况下A套餐更省钱？

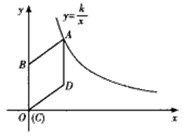
如图，在平面直角坐标系中，菱形ABCD的顶点C与原点O重合，点B在y轴的正半轴上，点A在函数y=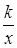（k>0,x>0）的图象上，点D的坐标为（4，3）．
（1）求k的值；
（2）若将菱形ABCD沿x轴正方向平移，当菱形的顶点D落在函数y=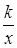（k>0,x>0）的图象上时，求菱形ABCD沿x轴正方向平移的距离．

试卷网试题网古诗词网作文网范文网