已知 的内切圆 与 、 、 分别相切于点 、 、 ,若 ,如图1.
(1)判断 的形状,并证明你的结论;
(2)设 与 相交于点 ,如图2, ,求 的长.

某村有一口水井,水面比井口低3米,一只蜗牛从水面沿着井壁竖直向井口爬,第一次向上爬了0.5米后又向下滑了0.1米;第二次向上爬了0.42米后却又向下滑了0.15米;第三次向上爬了0.7米后却又向下滑了0.15米;第四次向上爬了0.75米后却又向下滑了0.1米;第五次向上爬了0.55米后没有下滑;第六次向上爬了0.48米,问蜗牛有没有爬出井口?
化简求值: ,其中
,其中
如图:
(1)在数轴上标出表示-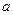 、-b的点;
、-b的点;
(2)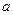 0;b 0;│
0;b 0;│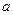 ││b│;
││b│;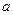 -b 0
-b 0
(3)用“<”号把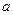 、b、0、-
、b、0、-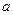 、-b连接起来.
、-b连接起来.
如图9,边长为5的正方形 的顶点
的顶点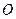 在坐标原点处,点
在坐标原点处,点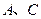 分别在
分别在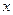 轴、
轴、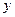 轴的正半轴上,点
轴的正半轴上,点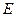 是
是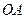 边上的点(不与点
边上的点(不与点 重合),
重合), ,且与正方形外角平分线
,且与正方形外角平分线 交于点
交于点 .
.
(1)当点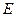 坐标为
坐标为 时,试证明
时,试证明 ;
;
(2)如果将上述条件“点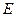 坐标为(3,0)”改为“点
坐标为(3,0)”改为“点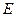 坐标为(
坐标为(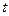 ,0)(
,0)(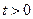 )”,结论
)”,结论 是否仍然成立,请说明理由;
是否仍然成立,请说明理由;
(3)在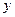 轴上是否存在点
轴上是否存在点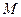 ,使得四边形
,使得四边形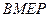 是平行四边形?若存在,用
是平行四边形?若存在,用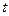 表示点
表示点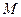
的坐标;若不存在,说明理由.
已知二次函数 的图象经过
的图象经过 和
和 三点
三点
(1)若该函数图象顶点恰为点 ,写出此时
,写出此时 的值及
的值及 的最大值;
的最大值;
(2)当 时,确定这个二次函数的解析式,并判断此时
时,确定这个二次函数的解析式,并判断此时 是否有最大值;
是否有最大值;
(3)由(1)、(2)可知, 的取值变化,会影响该函数图象的开口方向.请你求出
的取值变化,会影响该函数图象的开口方向.请你求出 满足
满足
什么条件时, 有最小值?
有最小值?