如图1所示，将一个边长为2的正方形ABCD和一个长为2、宽为1的长方形CEFD拼在一起，构成一个大的长方形ABEF．现将小长方形CEFD绕点C顺时针旋转至CE′F′D′，旋转角为a．
（1）当点D′恰好落在EF边上时，求旋转角a的值；
（2）如图2，G为BC中点，且0°＜a＜90°，求证：GD′=E′D；
（3）小长方形CEFD绕点C顺时针旋转一周的过程中，△DCD′与△CBD′能否全等？若能，直接写出旋转角a的值；若不能说明理由．
甲、乙两名运动员进行长跑训练，两人距终点的路程y（米）与跑步时间x之间的函数图象如图所示，根据图象所提供的信息解答问题：
（1）他们在进行米的长跑训练，在0＜x＜15的时段内，速度较快的人是；
（2）求甲距终点的路程y（米）和跑步时间x之间的函数关系式；
（3）当x=15时，两人相距多少米？在15＜x＜20的时段内，求两人速度之差．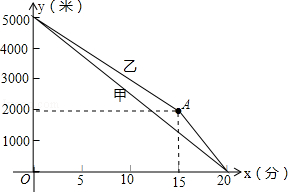
解不等式组：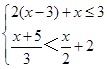
，且写出使不等式组成立的所有整数．
先化简，再求值：
，其中
．
如图，已知∠MON两边分别为OM、ON，sin∠O=
且OA=5，点D为线段OA上的动点（不与O重合），以A为圆心、AD为半径作⊙A，设OD=x．
（1）若⊙A交∠O 的边OM于B、C两点，BC=y，求y关于x的函数解析式，并写出函数的定义域；
（2）将⊙A沿直线OM翻折后得到⊙A′．
①若⊙A′与直线OA相切，求x的值；
②若⊙A′与以D为圆心、DO为半径的⊙D相切，求x的值．
如图，直线y=4x+4与x轴、y轴相交于B、C两点，抛物线y=ax2-2ax+c（a≠0）过点B、C，且与x轴另一个交点为A，以OC、OA为边作矩形OADC，CD交抛物线于点G．
（1）求抛物线的解析式以及点A的坐标；
（2）已知直线x=m交OA于点E，交CD于点F，交AC于点M，交抛物线（CD上方部分）于点P，请用含m的代数式表示PM的长；
（3）在（2）的条件下，联结PC，若△PCF和△AEM相似，求m的值．