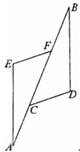
如图,抛物线 与 轴交于 , 两点,与 轴的正半轴交于点 ,其顶点为 .
(1)写出 , 两点的坐标(用含 的式子表示);
(2)设 ,求 的值;
(3)当 是直角三角形时,求对应抛物线的解析式.

为了掌握我市中考模拟数学考试卷的命题质量与难度系数,命题教师赴我市某地选取一个水平相当的初三年级进行调研,命题教师将随机抽取的部分学生成绩(得分为整数,满分为150分)分为5组:第一组75~90;第二组90~105;第三组105~120;第四组120~135;第五组135~150.统计后 得到如图所示的频数分布直方图(每组含最小值不含最大值)和扇形统计图.观察图形的信息,回答下列问题: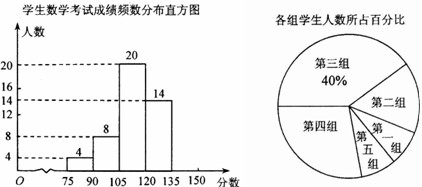

(1)本次调查共随机抽取了该年级____名学生,并将频数分布直方图补充完整:
(2)若将得分转化为等级,规定:得分低于 90分评为“D”,90~120 分评为“C”,120~135分评为 “B”,135~150分评为“A”.那么该年级 1500名考生中,考试成绩评为“B”的学生 名;
(3)如果第一组只有一名是女生,第五组只有一名是男生,针对考试成绩情况,命题教师决定从第一组、第五组分别随机选出一名同学谈谈做题的感想.请你用列表或画树状图的方法求出所选两名 学生刚好是一名女生和一名男生的概率.
如图,在平面直角坐标系 中,一次函数
中,一次函数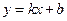 与反比例函数
与反比例函数 的图象交于点
的图象交于点 ,与
,与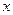 轴交于点
轴交于点 ,
, 轴于点
轴于点 ,
,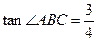 ,
, ,
,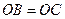 。
。
(1)求反比例函数和一次函数的解析式;
(2)若一次函数与反 比例函数的图象的另一交点为点
比例函数的图象的另一交点为点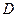 ,连接
,连接 、
、 ,求
,求
先化简,再求值: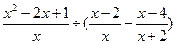 ,其中
,其中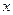 满足
满足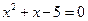 。
。
为促进“平安重庆”建设,市公安局交巡警总队拟在我市某“三角形”转盘区域内新增一个交巡警平 台,使交巡警平台到三个十字路 a 的距离相等,试确定交巡警平台 P的位置.(要求:用尺规作图, 保留作图痕迹,不写已知、求作和作法).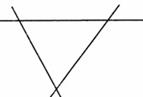
如图,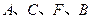 在同一直线上,
在同一直线上,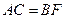 ,
,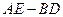 ,且
,且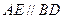 。求证:
。求证: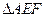 与
与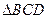 全等。
全等。