已知抛物线 与 轴交于点 和点 .
(1)求抛物线 的函数解析式;
(2)如图①,将抛物线 沿 轴翻折得到抛物线 ,抛物线 与 轴交于点 ,点 是线段 上的一个动点,过点 作 轴交抛物线 于点 ,求线段 的长度的最大值;
(3)在(2)的条件下,当线段 处于长度最大值位置时,作线段 的垂直平分线交 于点 ,垂足为 ,点 是抛物线 上一动点, 与直线 相切,且 ,求满足条件的所有点 的坐标.

如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,有下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF.
其中正确结论的序号是(把你认为正确的都填上).
如图,在△ABC中,AD平分∠BAC,DE∥AC交AB于点E,M是AD的中点,延长EM交AC于F.
求证:AD垂直平分线段EF.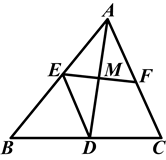
如图,在△ABC中,∠BAC=90°,AH⊥BC于H,∠ABC的平分线交AC于D,交AH于E,DF⊥BC于F.求证:四边形AEFD是菱形.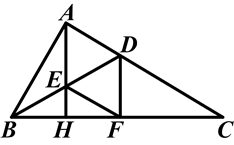
如图,在菱形ABCD中,E是AB的中点,且DE⊥AB,AB=10.
(1)求∠ABC的度数;
(2)求对角线AC的长度;
(3)求菱形ABCD的面积.
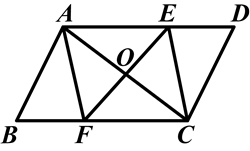
如图,□ABCD的对角线AC的垂直平分线与AD、BC、AC分别交于点E、F、O,求证:四边形AFCE是菱形.