直线 的解析式为 ，分别交 轴、 轴于点 ， ．
（1）写出 ， 两点的坐标，并画出直线 的图象；
（2）将直线 向上平移4个单位得到 ， 交 轴于点 ．作出 的图象， 的解析式是 ．
（3）将直线 绕点 顺时针旋转 得到 ， 交 于点 ．作出 的图象， ．
(6分) 如图①、图②、图③……是用围棋子摆成的一列具有一定规律的“山”字．
(5)按图示的规律填空．
| 图形标号 |
① |
② |
③ |
④ |
…… |
| 围棋子的数目(颗) |
7 |
(6)第n个图形所对应的围棋子的数目为___________颗．
若某个图形中有围棋子142颗，它是第__________个图形．
(6分) 已知a、b互为相反数，c、d互为倒数，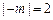
，
求代数式：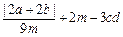
的值．
先化简，再求值：（每小题6分，共12分）
（1）
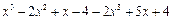，其中x =" –" 2；
（2）
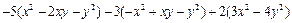，其中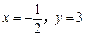
计算：（每小题6分，共24分）
(1)
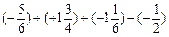
(2)
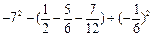
(3)
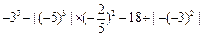
(4)
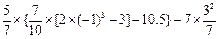
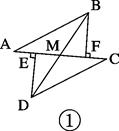
(9分) 如图①，E、F分别为线段AC上的两个动点，且DE⊥AC于E，
BF⊥AC于F，若AB=CD，AF=CE，BD交AC于点M。
（1）求证：MB=MD，ME=MF
（2）当E、F两点移动到如图②的位置时，其余条件不变，上述结论能否成立？若成立请给予证明；若不成立请说明理由。
