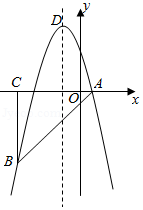
如图,在平面直角坐标系中, 为等腰直角三角形, ,抛物线 经过 , 两点,其中点 , 的坐标分别为 , ,抛物线的顶点为点 .
(1)求抛物线的解析式;
(2)点 是直角三角形 斜边 上的一个动点(不与 , 重合),过点 作 轴的垂线,交抛物线于点 ,当线段 的长度最大时,求点 的坐标;
(3)在(2)的条件下,抛物线上是否存在一点 ,使 是以 为直角边的直角三角形?若存在,求出所有点 的坐标;若不存在,请说明理由.
“端午”节前,第一次爸爸去超市购买了大小、质量都相同的火腿粽子和豆沙粽子若干,放入不透明的盒中,此时随机取出火腿粽子的概率为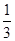 ;妈妈发现小亮喜欢吃的火腿粽子偏少,第二次妈妈又去买了同样的5只火腿粽子和1只豆沙粽子放入同一盒中,这时随机取出火腿粽子的概率为
;妈妈发现小亮喜欢吃的火腿粽子偏少,第二次妈妈又去买了同样的5只火腿粽子和1只豆沙粽子放入同一盒中,这时随机取出火腿粽子的概率为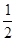
(1)请计算出第一次爸爸买的火腿粽子和豆沙粽子各有多少只?
(2)若妈妈从盒中取出火腿粽子6只、豆沙粽子7只送爷爷和奶奶后,再让小亮从盒中不放回地任取2只,问恰有火腿粽子、豆沙粽子各1只的概率是多少?
在学习“轴对称现象”内容时,王老师让同学们寻找身边的轴对称图形,小明有一副三角尺和一个量角器(如图所示).
(1)小明的这三件文具中,可以看做是轴对称图形的是___________(填字母代号);
(2)小红也有同样的一副三角尺和一个量角器.若他们分别从自己这三件文具中随机取出一件,则可以拼成一个轴对称图案的概率是多少?
如图,在△ABC中,AC=AB=2,∠A=90°,将一块与△ABC全等的三角板的直角顶点放在点C上,一直角边与BC重叠.
(1)操作1:固定△ABC,将三角板沿C→B方向平移,使其直角顶点落在BC的中点M,如图2所示,探究:三角板沿C→B方向平移的距离为 ;
(2)操作2:在(1)的情况下,将三角板BC的中点M顺时针方向旋转角度a(0°<a<90°),如图3所示,探究:设三角形板两直角边分别与AB、AC交于点P、Q,观察四边形MPAQ形状的变化,问:四边形MPAQ的面积S是否改变,若不变,求其面积;若改变,试说明理由;
(3)在(2)的情形下,连PQ,设BP=x,记△MPQ的面积为y,试求y关于x的函数关系式,并求x为何值时,y的值是四边形MPAQ的面积的一半,此时,指出四边形MPAQ的形状.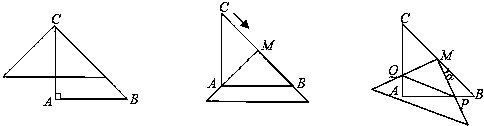
在一块长32m,宽24m的矩形荒地上建造一个花园,要求花轩占地面积为荒地面积的一半,下面分别是小强和小颖的设计方案.
说明:小强的设计方案如图(1),其中花园四周小路的宽度一样,通过解方程得到小路的宽为4m或24m,小颖的设计方案如图(2),其中每个角上的扇形半径都相同.
(1)你认为小强的结果对吗?请说明理由.
(2)请你帮助小颖求出图中的x.(π的值取3结果保留根号)
(3)你还有其他的设计方案吗?请在图(3)中画出一个与图(1)(2)有共同特点的设计草图,并加以说明.
在网格图中,每个小正方形的边长均为1个单位,在Rt△ABC中,∠C=90°,AC=3,BC=6.
(1)试作出△ABC以A为旋转中心、沿顺时针方向旋转90°后的图形△AB′C′;
(2)若点B的坐标为(-4,5),试建立合适的直角坐标系,并写出A、C两点的坐标;
(3)作出与△ABC关于原点对称的图形△A″B″C″,并写出A″、B″、C″三点的坐标.