某商店计划购进甲、乙两种笔记本,已知2本甲笔记本与3本乙笔记本的总进价为42元,2本甲笔记本与1本乙笔记本的总进价为22元.
(1)求甲、乙两种笔记本的进价分别是多少元?
(2)该商店计划购进两种笔记本共40本,其中甲笔记本的数量不超过乙笔记本的数量,且总金额不超过330元,求共有几种进货方案,并指出哪种方案最省钱.
如图,四边形ABCD中,∠A=90°,AD∥BC,BE⊥CD
于E交AD的延长线于F,DC=2AD,AB=BE.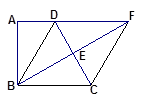
求证:AD=DE
判断四边形BCFD的形状并说明理由.
如图,在一次课外数学实践活动中,小明站在操场的A处,他的两侧分别是旗杆CD和一幢教学楼EF,点A、D、F在同一直线上,从A处测得旗杆顶部和教学楼顶部的仰角分别为45°和60°,已知DF=14m,EF=15m,求旗杆CD高.(结果精确到0.1m,参考数据:
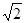 ≈1.41,
≈1.41,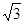 ≈1.73)
≈1.73)
如图1,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高(h)”.我们可得出一种计算三角形面积的新方法: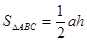 ,即三角形面积等于水平宽与铅垂高乘积的一半.
,即三角形面积等于水平宽与铅垂高乘积的一半.
解答下列问题:
如图2,抛物线顶点坐标为点C(1,4),交x轴于点A(3,0),交y轴于点B.
(1)求抛物线和直线AB的解析式;
(2)点P是抛物线(在第一象限内)上的一个动点,连结PA,PB,当P点运动到顶点C时,求△CAB的铅垂高CD及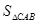 ;
;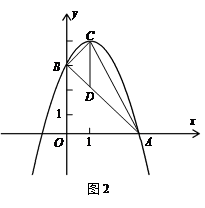 (3)是否存在一点P,使S△PAB=
(3)是否存在一点P,使S△PAB=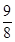 S△CAB,若存在,求出P点的坐标;若不存在,请说明理由.
S△CAB,若存在,求出P点的坐标;若不存在,请说明理由.
我们知道当人的视线与物体表面互相垂直时的视觉效果最佳.如图是小明站在距离墙壁1.60米处观察装饰画时的示意图,此时小明的眼睛与装饰画底部A处于同一水平线上,视线恰好落在装饰画中心位置E处,且与AD垂直.已知装饰画的高度AD为0.66米,
求:⑴ 装饰画与墙壁的夹角∠CAD的度数(精确到1°);
⑵ 装饰画顶部到墙壁的距离DC(精确到0.01米).
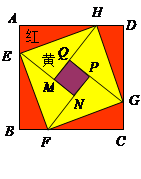
某数学研究所门前有一个边长为4米的正方形花坛,花坛内部要用红、黄、紫三种颜色的花草种植成如图所示的图案,图案中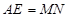 .准备在形如Rt
.准备在形如Rt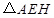 的四个全等三角形内种植红色花草,在形如Rt△EMH的四个全等三角形内种植黄色花草,在正方形
的四个全等三角形内种植红色花草,在形如Rt△EMH的四个全等三角形内种植黄色花草,在正方形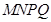 内种植紫色花草,每种花草的价格如下表:
内种植紫色花草,每种花草的价格如下表:
| 品种 |
红色花草 |
黄色花草 |
紫色花草 |
| 价格(元/米2) |
60 |
80 |
120 |
设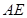 的长为
的长为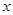 米,正方形
米,正方形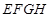 的面积为
的面积为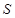 平方米,买花草所需的费用为
平方米,买花草所需的费用为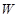 元,解答下列问题:
元,解答下列问题:
(1)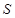 与
与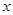 之间的函数关系式为
之间的函数关系式为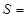 ;
;
(2)求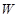 与
与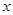 之间的函数关系式,并求所需的最低费用是多少元;
之间的函数关系式,并求所需的最低费用是多少元;
(3)当买花草所需的费用最低时,求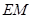 的长.
的长.