某数学研究所门前有一个边长为4米的正方形花坛，花坛内部要用红、黄、紫三种颜色的花草种植成如图所示的图案，图案中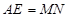
．准备在形如Rt
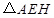的四个全等三角形内种植红色花草，在形如Rt△EMH的四个全等三角形内种植黄色花草，在正方形
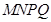内种植紫色花草，每种花草的价格如下表：
| 品种 |
红色花草 |
黄色花草 |
紫色花草 |
| 价格（元/米2） |
60 |
80 |
120 |
设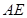
的长为
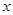米，正方形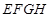
的面积为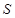
平方米，买花草所需的费用为
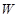元，解答下列问题：
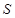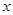（1）与之间的函数关系式为
；
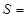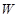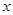（2）求与之间的函数关系式，并求所需的最低费用是多少元；
（3）当买花草所需的费用最低时，求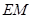
的长．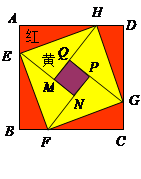
【原创题】我校数学兴趣小组为了解泌园牌净水机的销售情况，对我市泌园牌净水机专卖店第一季度A、B、C、D四种型号的销量做了统计，绘制成如下两幅统计图（均不完整）。
（1）该店第一季度售出泌园牌净水机共多少台？
（2）把两幅统计图补充完整；
（3）若该专卖店计划订购这四款型号泌园牌净水机900辆，求C型泌园牌净水机订购多少辆？
【原创题】先化简，再求值
，其中x=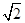
．
如图，排球运动员站在点O处练习发球，将球从O点正上方2m的A处发出，把球看成点，其运行的高度y（m）与运行的水平距离x（m）满足关系式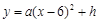
，已知球网与O点的水平距离为9m，球网高度为2．43m，球场另一边的底线距O点的水平距离为18m．
（1）当h=2．6时，求y与x的关系式（不要求写出自变量x的取值范围）
（2）当h=2．6时，球能否越过球网？球会不会出底线？请说明理由；
（3）若球一定能越过球网，且刚好落在底线上，求h的值．
【改编题】已知：如图，在Rt△ABC中，∠C=90°，点E在斜边AB上，以AE为直径的⊙O与BC边相切于点D，连接AD．
（1）求证：AD是∠BAC的平分线；
（2）若AC=3，tanB=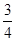
，求⊙O的半径．
【改编题】如图（1），在等边的顶点B、C处各有一只蜗牛，它们同时出发△ABC分别以每分钟1各单位的速度油B向C和由C向A爬行，其中一只蜗牛爬到终点s时，另一只也停止运动，经过t分钟后，它们分别爬行到D，P处，请问：
（1）在爬行过程中，BD和AP始终相等吗？为什么？
（2）问蜗牛在爬行过程中BD与AP所成的∠DQA大小有无变化？请证明你的结论．
（3）若蜗牛沿着BC和CA的延长线爬行，BD与AP交于点Q，其他条件不变，如图（2）所示，蜗牛爬行过程中的∠DQA大小变化了吗？若无变化，请证明．若有变化，请直接写出∠DQA的度数．