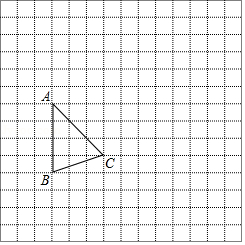
如图,在网格中,每个小正方形的边长均为1个单位长度.我们将小正方形的顶点叫做格点, 的三个顶点均在格点上.
(1)将 先向右平移6个单位长度,再向上平移3个单位长度,得到△ ,画出平移后的△ ;
(2)建立适当的平面直角坐标系,使得点 的坐标为 ;
(3)在(2)的条件下,直接写出点 的坐标.
甲乙两组工人同时开始加工某种零件,乙组在工作中有一次停产更换设备,更换设备后,乙组的工作效率是原来的2倍.两组各自加工零件的数量y(件)与时间x(时)之间函数图象如图所示.
(1)求数量y与时间x之间函数关系式.
(2)求乙组加工零件总量a值.
(3)甲乙两组加工出的零件合在一起装箱,每够300件装一箱,装箱时间忽略不计,求经过多长时间恰好装满第1箱?再经过多长时间恰好装满第2箱?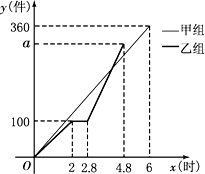
如图所示.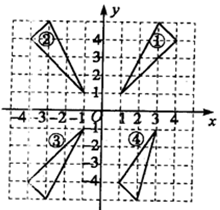
(1)写出三角形③的顶点坐标.
(2)通过平移由③能得到④吗?为什么?
(3)根据对称性由三角形③可得三角形①、②,顶点坐标各是什么?
已知:把Rt△ABC和Rt△DEF按如图(1)摆放(点C与点E重合),点B、C(E)、F在同一条直线上.∠ACB = ∠EDF = 90°,∠DEF = 45°,AC =" 8" cm,BC =" 6" cm,EF =" 9" cm。
如图(2),△DEF从图(1)的位置出发,以1 cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△ABC的顶点B出发,以2 cm/s的速度沿BA向点A匀速移动。当△DEF的顶点D移动到AC边上时,△DEF停止移动,点P也随之停止移。DE与AC相交于点Q,连接PQ,设移动时间为t(s)(0<t<4.5)。解答下列问题:
(1)当t为何值时,点A在线段PQ的垂直平分线上?
(2)连接PE,设四边形APEC的面积为y(cm2),求y与t之间的函数关系式;是否存在某一时刻t,使面积y最小?若存在,求出y的最小值;若不存在,说明理由。
(3)是否存在某一时刻t,使P、Q、F三点在同一条直线上?若存在,求出此时t的值;若不存在,说明理由。(图(3)供同学们做题使用)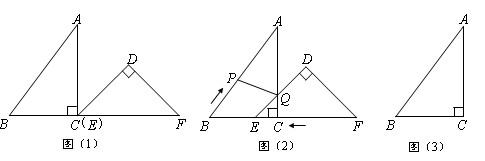
如图, 已知抛物线 与y轴相交于C,与x轴相交于A、B,点A的坐标为(2,0),点C的坐标为(0,-1)。
与y轴相交于C,与x轴相交于A、B,点A的坐标为(2,0),点C的坐标为(0,-1)。
(1)求抛物线的解析式;
(2)点E是线段AC上一动点,过点E作DE⊥x轴于点D,连结DC,当△DCE的面积最大时,求点D的坐标;
(3)在直线BC上是否存在一点P,使△ACP为等腰三角形,若存在,求点P的坐标,若不存在,说明理由。
如图,在正方形ABCD中,E、F分别为BC、AB上两点,且BE=BF,过点B作AE的垂线交AC于点G,过点G作CF的垂线交BC于点H延长线段AE、GH交于点M.
(1)求证:∠BFC=∠BEA;
(2)求证:AM=BG+GM。