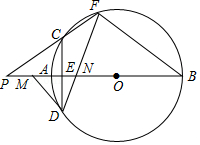
如图, 是 的直径,弦 于点 ,点 是 上一点,且 ,连接 , , 交 于点 .
(1)若 , ,求 的半径;
(2)求证: 为等腰三角形;
(3)连接 并延长,交 的延长线于点 ,过点 作 的切线,交 的延长线于点 .求证: .
△ABC在平面直角坐标系中的位置如图所示.
(1)作出△ABC关于 轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标;
轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标;
(2)将△ABC向右平移6个单位,作出平移后的△A2B2C2,并写出△A2B2C2各顶点的坐标;
(3)观察△A1B1C和△A2B2C2,它们是否关于某直线对称?若是,请用粗线条画出对称轴并写出来.
如图,在△ABC中,∠B=30°,∠C=66°,AE⊥BC于E,AD平分∠BAC,求∠DAE的度数.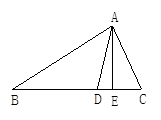
已知y+4与x-3成正比例,且x=5时y=4.
(1)求y与x之间的函数关系式;
(2)当y=4时,求x的值.
(本题12分)射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2cm,
QM=4cm.动点P从点Q出发,沿射线QN以每秒1cm的速度向右移动,经过t秒,以点P为圆心,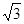 cm
cm
为半径的圆与△ABC的边相切(切点在边上),求t值(单位:秒).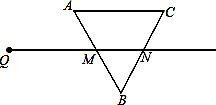
(本题12分))如图,点B、C、D都在⊙O上,过点C作AC∥BD交OB延长线于点A,连接CD,且∠CDB=∠OBD=30°,DB=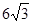 cm.
cm.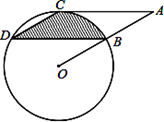
(1)直线AC与⊙O有怎样的位置关系?为什么?
(2)求由弦CD、BD与弧BC所围成的阴影部分的面积.(结果保留π)