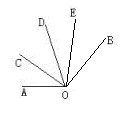
如图,直角 中, 为直角, , .点 , , 分别在 , , 边上同时开始作匀速运动,2秒后三个点同时停止运动,点 由点 出发以每秒3个单位的速度向点 运动,点 由点 出发以每秒5个单位的速度向点 运动,点 由点 出发以每秒4个单位的速度向点 运动,在运动过程中:
(1)求证: , , 的面积相等;
(2)求 面积的最小值;
(3)用 (秒 表示运动时间,是否存在 ,使 ?若存在,请直接写出 的值;若不存在,请说明理由.

一家商店将某种服装按进价提高40%后标价,又以8折优惠卖出,结果每件仍获利15元,这种服装每件的进价是多少?
一个三位数,三个数位上的数字之和是17,百位上的数比十位上的数大7,个位上的数是十位上的数的3倍,求这个三位数
某学校今年为山区捐款28000元,比去年的2倍还多500元,去年该学校为山区捐款多少元?
OM是∠AOB的平分线,射线OC在∠BOM内,ON是∠BOC的平分线,已知∠AOC=80º,那么∠MON的度数是多少?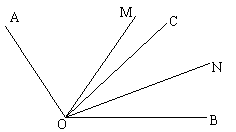
如图,OC是∠AOD的平分线,OE是∠BOD的平分线。(1)如果∠AOB=130°,那么∠COE是多少度? (2)如果∠COE=65°,∠COD=20°,那么∠BOE是多少度?