(1)阅读理解:
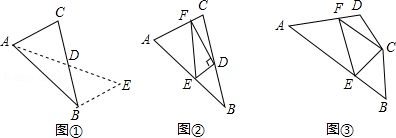
如图①,在 中,若 , ,求 边上的中线 的取值范围.
解决此问题可以用如下方法:延长 到点 使 ,再连接 (或将 绕着点 逆时针旋转 得到 ,把 、 , 集中在 中,利用三角形三边的关系即可判断.
中线 的取值范围是 ;
(2)问题解决:
如图②,在 中, 是 边上的中点, 于点 , 交 于点 , 交 于点 ,连接 ,求证: ;
(3)问题拓展:
如图③,在四边形 中, , , ,以 为顶点作一个 角,角的两边分别交 , 于 、 两点,连接 ,探索线段 , , 之间的数量关系,并加以证明.
若函数y=kx+b的图像经过点(-3,-2)和(1,6)求k、b及函数关系式。
如图,AD是△ABC的∠BAC的平分线,DE、DF分别是△ABD和△ACD的高,求证:AD是EF的垂直平分线.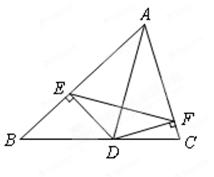
(10分) 如图,AD是∠BAC的平分线,DE⊥AB于点E,DF⊥AC于点F,且DB=DC。求:BE=CF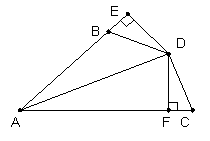
如图,已知:∠CAE是△ABC的外角,AD是∠CAE的平分线,AD∥BC 。求证:AB=AC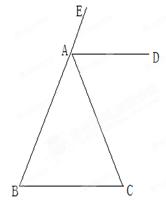
小明的爷爷吃过晚饭后,出门散步,再报亭看了一会儿报纸才回家,小明绘制了爷爷离家的路程s(米)与外出的时间t之间的关系图。根据图像回答下列问题:
(1)报亭离爷爷家________米;
(2)爷爷在报亭看了________分钟报纸;
(3)爷爷走去报亭的平均速度是________米∕分。