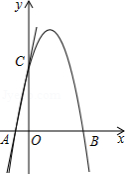
如图,直线 交 轴于点 ,交 轴于点 ,过 , 两点的二次函数 的图象交 轴于另一点 .
(1)求二次函数的表达式;
(2)连接 ,点 是线段 上的动点,作 轴交二次函数的图象于点 ,求线段 长度的最大值;
(3)若点 为二次函数 图象的顶点,点 是该二次函数图象上一点,在 轴、 轴上分别找点 , ,使四边形 的周长最小,求出点 , 的坐标.
温馨提示:在直角坐标系中,若点 , 的坐标分别为 , , , ,
当 平行 轴时,线段 的长度可由公式 求出;
当 平行 轴时,线段 的长度可由公式 求出.
胡老师计划组织朋友暑假去革命圣地延安两日游,经了解,现有甲、乙两家旅行社比较合适,报价均为每人640元,且提供的服务完全相同,针对组团两日游的游客,甲旅行社表示,每人都按八五折收费;乙旅行社表示,若人数不超过20人,每人都按九折收费,超过20人,则超出部分每人按七五折收费。假设组团参加甲、乙两家旅行社两日游的人数均为x人。
(1)请分别写出甲、乙两家旅行社收取组团两日游的总费用y(元)与x(人)之间的函数关系式;
(2)若胡老师组团参加两日游的人数共有32人,请你通过计算,在甲、乙两家旅行社中,帮助胡老师选择收取总费用较少的一家。
在平面直角坐标系xOy中,过点(0,2)且平行于x轴的直线,与直线y=x-1交于点A,点A关于直线x=1的对称点为B,抛物线C1:y=x2+bx+c经过点A,B.
(1)求点A,B的坐标;
(2)求抛物线C1的表达式及顶点坐标;
(3)若拋物线C2:y=ax2(a≠0)与线段AB恰有一个公共点,结合函数的图象,求a的取值范围.
作平面直角坐标系xOy中,直线y=kx+b(k≠0)与双曲线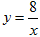 的一个交点为P(2,m),与x轴、y轴分别交于点A,B.
的一个交点为P(2,m),与x轴、y轴分别交于点A,B.
(1)求m的值;
(2)若PA=2AB,求k的值.
(本小题10分)
已知二次函数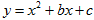 ( b,c为常数).
( b,c为常数).
(Ⅰ)当b =2,c =-3时,求二次函数的最小值;
(Ⅱ)当c =5时,若在函数值y =1的情况下,只有一个自变量x的值与其对应,求此时二次函数的解析式;
(Ⅲ)当c=b2时,若在自变量x的值满足b≤x≤b+3的情况下,与其对应的函数值y的最小值为21,求此时二次函数的解析式.
(本小题满分11分)
如图,已知点O(0,0),A(-5,0),B(2,1),抛物线l:y=-(x-h)2+1(h为常数)与y轴的交点为C.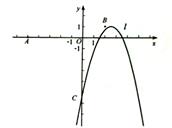
(1)l经过点B,求它的解析式,并写出此时l的对称轴及顶点坐标:
(2)设点C的级坐标为yc,求yc的最大值,此时l上有两点(x1,y1),(x2,y2),其中x1>x2≥0,比较y1与y1的大小;
(3)当线段OA被l只分为两部分,且这两部分的比是1:4时,求h的值.