凯里市某文具店某种型号的计算器每只进价12元，售价20元，多买优惠，优惠方法是：凡是一次买10只以上的，每多买一只，所买的全部计算器每只就降价0.1元，例如：某人买18只计算器，于是每只降价 （元 ，因此所买的18只计算器都按每只19.2元的价格购买，但是每只计算器的最低售价为16元．
（1）求一次至少购买多少只计算器，才能以最低价购买？
（2）求写出该文具店一次销售 只时，所获利润 （元 与 （只 之间的函数关系式，并写出自变量 的取值范围；
（3）一天，甲顾客购买了46只，乙顾客购买了50只，店主发现卖46只赚的钱反而比卖50只赚的钱多，请你说明发生这一现象的原因；当 时，为了获得最大利润，店家一次应卖多少只？这时的售价是多少？
已知关于x的方程x2-（k+2）x+2k=0．
（1）小明同学说：“无论k取何实数，方程总有实数根。”你认为他说的有道理吗？并说明理由。
（2）若等腰三角形的一边长a=1，另两边长b、c恰好是这个方程的两个根，求△ABC的周长。
先化简，再求值：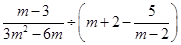
，其中m是方程
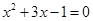的根．
解下列方程
（1）
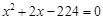
（2）
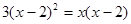
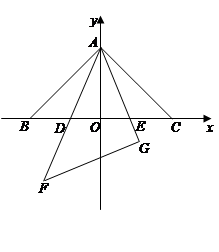
如图，在同一平面内，将两个全等的等腰直角三角形ABC和AFG摆放在一起，A为公共顶点，∠BAC=∠AGF=90°，它们的斜边长为2，若∆ABC固定不动，∆AFG绕点A旋转，AF、AG与边BC的交点分别为D、E（点D不与点B重合，点E不与点C重合），设BE=m，CD=n．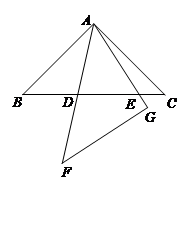
（1）请在图中找出两对相似而不全等的三角形，并选取其中一对进行证明．
（2）求m与n的函数关系式，直接写出自变量n的取值范围．
（3）以∆ABC的斜边BC所在的直线为x轴，BC边上的高所在的直线为y轴，建立平面直角坐标系（如图12）．在边BC上找一点D，使BD=CE，求出D点的坐标，并通过计算验证BD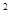
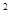＋CE=DE．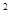
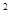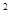（4）在旋转过程中，（3）中的等量关系BD＋CE=DE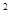是否始终成立，若成立，请证明，若不成立，请说明理由．
某检修小组乘汽车检修公路道路．向东记为正，向西记为负．某天自A地出发．所走路程（单位：千米）为：+2，-3，+4，-2，-8，0，-4，-3
问：（1）最后他们在A地的什么地方？距离A地多远？
（2）若每千米耗油0．05升，则今天共耗油多少升？