随着交通道路的不断完善，带动了旅游业的发展，某市旅游景区有 、 、 、 、 等著名景点，该市旅游部门统计绘制出2017年“五 一”长假期间旅游情况统计图，根据以下信息解答下列问题：
（1）2017年“五 一”期间，该市周边景点共接待游客 万人，扇形统计图中 景点所对应的圆心角的度数是 ，并补全条形统计图．
（2）根据近几年到该市旅游人数增长趋势，预计2018年“五 一”节将有80万游客选择该市旅游，请估计有多少万人会选择去 景点旅游？
（3）甲、乙两个旅行团在 、 、 三个景点中，同时选择去同一景点的概率是多少？请用画树状图或列表法加以说明，并列举所有等可能的结果．
为了解学生课余活动情况，某校对参加绘画、书法、舞蹈、乐器这四个课外兴趣小组的人员分布情况进行抽样调查，并根据收集的数据绘制了下面两幅不完整的统计图，请根据图中提供的信息，解答下面的问题：
（1）此次共调查了多少名同学？
（2）将条形统计图补充完整，并计算扇形统计图中书法部分的圆心角的度数；
（3）如果该校共有
名学生参加这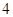
个课外兴趣小组，面每位教师最多只能辅导本组的
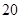名学生，估计每个兴趣小组至少需要准备多少名教师．
张师傅根据某直三棱柱零件，按1：1的比例画出准确的三视图如下：已知△EFG中，EF="4" cm，∠EFG=45°，FG="10" cm，AD="12" cm．（1）求AB的长；（2）直接写出这个直三棱柱的体积．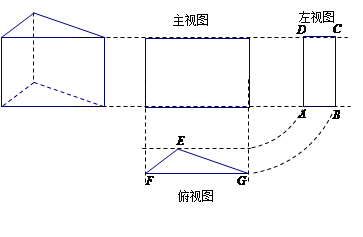
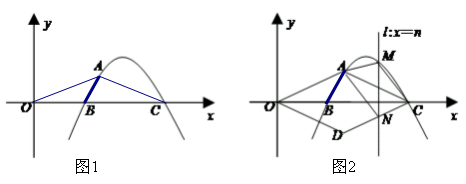
如图1，抛物线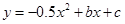
与x轴交于B(3,0) 、C(8.0)两点，抛物线另有一点A在第一象限内，连接AO、AC，且AO=AC.求抛物线的解析式；
将△OAC绕x轴旋转一周，求所得旋转体的表面积；
如图2，将△OAC沿x轴翻折后得△ODC，设垂直于x轴的直线l：x＝n与（1）中所求的抛物线交于点M，与CD交于点N，若直线l 沿x轴方向左右平移，且交点M始终位于抛物线上A、C两点之间时，试探究：当n为何值时，四边形AMCN的面积取得最大值，并求出这个最大值．
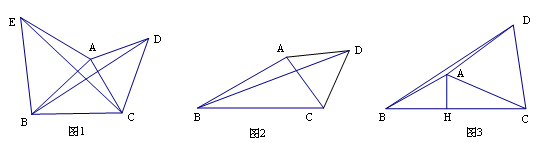
已知△ABC，以AC为边在△ABC外作等腰△ACD，其中AC=AD。如图1，以AB为边在△ABC外作等腰△ABE，其中AB=AE，，试证明BD=CE；
如图2，若∠ABC=30°，△ACD是等边三角形，AB=3，BC=4，求BD的长；
如图3，若∠ACB为锐角，作AH⊥BC于H，当BD2=4AH2+BC2时，问∠DAC与∠ABC有怎样的关系，直接写出结论（不需要证明）。
现计划把甲种货物1240吨和乙种货物880吨用一列货车运往某地，已知这列货车挂有A、B两种不同规格的货车厢共40节，使用A型车厢每节费用为0.6万元，使用B型车厢每节费用为0.8万元．设运送这批货物的总费用为y万元，这列货车挂A型车厢x节，试写出y与x之间的函数关系式；
如果每节A型车厢最多可装甲种货物35吨和乙种货物15吨，每节B型车厢最多可装甲种货物25吨和乙种货物35吨，装货时按此要求安排A、B两种车厢的节数，那么共有哪几种安排车厢的方案？
在上述方案中，哪个方案运费最省？最少运费为多少元？