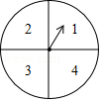
由于只有1张市运动会开幕式的门票，小王和小张都想去，两人商量采取转转盘（如图，转盘盘面被分为面积相等，且标有数字1，2，3，4的4个扇形区域）的游戏方式决定谁胜谁去观看．规则如下：两人各转动转盘一次，当转盘指针停止，如两次指针对应盘面数字都是奇数，则小王胜；如两次指针对应盘面数字都是偶数，则小张胜；如两次指针对应盘面数字是一奇一偶，视为平局．若为平局，继续上述游戏，直至分出胜负．
如果小王和小张按上述规则各转动转盘一次，则
（1）小王转动转盘，当转盘指针停止，对应盘面数字为奇数的概率是多少？
（2）该游戏是否公平？请用列表或画树状图的方法说明理由．
，
，
，
，
，
，
，求代数式
的值.