一副直角三角板（其中一个三角板的内角是45°，45°，90°，另一个是30°，60°，90°）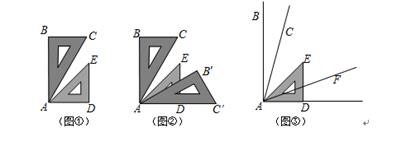
（1）如图①放置，AB⊥AD，∠CAE= ，BC与AD的位置关系是 ；
（2）在（1）的基础上，再拿一个30°，60°，90°的直角三角板，如图②放置，将AC′边和AD边重合，AE是∠CAB′的角平分线吗，如果是，请加以说明，如果不是，请说明理由．
（3）根据（1）（2）的计算，请解决下列问题：如图③∠BAD=90°，∠BAC=∠FAD=20°，将一个45°，45°，90°直角三角板的一直角边与AD边重合，锐角顶点A与∠BAD的顶点重合，AE是∠CAF的角平分线吗？如果是，请加以说明，如果不是，请说明理由．
（4）如果将图③中的∠BAC=∠FAD=α（α是锐角），其它条件不变，那么（3）问中的结论还成立吗？只需回答是还是不是，不需要说明理由．
如图11-1，有一座抛物线型拱桥，涨潮时桥内水面宽AB为8米，落潮时水位下降5米，桥内水面宽CD为12米．
（1）建立适当的平面直角坐标系，并求此抛物线的解析式；
（2）如图11-2，某种货船在水面上的部分的横截面是梯形EFGH，且HE=FG，EF= 
HE，∠GHE=45°．试问落潮时，能顺利通过拱桥的这种货船在水面上的部分最大高度是多少？
如图10-1，在△A B B′和△A C C′中，∠B A B′=∠C A C′=m°，AC=AC'，AB=AB'．
（1）不添加辅助线的前提下，请写出图中满足旋转变换的两个三角形分别是：；旋转角度是°；
（2）线段BC、B'C'的数量关系是：；试求出BC、B'C'所在直线的夹角：；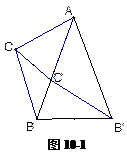
（3）随着△ACC'绕点A的旋转，（2）的结论是否依然成立？请从图10-2、图10-3中任选一个证明你的结论；
（4）利用解决上述问题所获得的经验探索下面的问题：如图10-4，等边△ABC外一点D，且∠BDC=60°,连接AD，试探索线段AD、CD、BD的数量关系．
某商店1月份开始营业并盈利1500元，3月份盈利2160元．如果该商店每个月盈利的月增长率相同，求：（1）该商店月平均增长率；（2）该商店第一季度共盈利多少元？
按要求解下列两个方程：
（1）
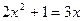（配方法）（2）
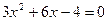（公式法）
某商场试销一种成本为每件60元的服装，规定试销期间销售单价不低于成本单价，且获利不得高于45%，经试销发现，销售量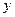
（件）与销售单价
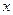（元）符合一次函数关系：
|
… |
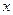60 |
65 |
70 |
75 |
80 |
… |
|
… |
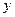60 |
55 |
50 |
45 |
40 |
… |
（1）求销售量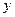与销售单价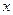的函数关系式；
（2）若该商场获得利润为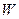
元，试写出利润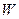与销售单价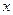之间的关系式；并求出销售单价定为多少元时，商场可获得最大利润，最大利润是多少元？
（3）若该商场获得利润不低于500元，试确定销售单价的范围．