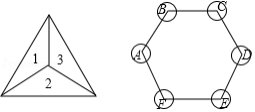
图①是一枚质地均匀的正四面体形状的骰子,每个面上分别标有数字1,2,3,4,图②是一个正六边形棋盘,现通过掷骰子的方式玩跳棋游戏,规则是:将这枚骰子掷出后,看骰子向上三个面(除底面外)的数字之和是几,就从图②中的 点开始沿着顺时针方向连续跳动几个顶点,第二次从第一次的终点处开始,按第一次的方法跳动.
(1)随机掷一次骰子,则棋子跳动到点 处的概率是
(2)随机掷两次骰子,用画树状图或列表的方法,求棋子最终跳动到点 处的概率.
如图所示,在菱形ABCD中,已知E是BC上一点,且AE=AB,∠EAD=2∠BAE,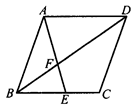
求证:BE=AF.
如图所示,在菱形ABCD中,BE⊥AD,BF⊥CD,E,F为垂足,AE=ED,求∠EBF的度数.
如图所示,在矩形ABCD中,对角线AC,BD交于点O,过顶点C作CE∥BD,交A孤延长线于点E,求证:AC=CE.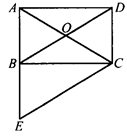
如图所示,在矩形ABCD中,点E在DC上,AE=2BC,且AE=AB,求∠CBE的度数.
如图所示,在矩形ABCD中,AB=5cm,BC=4cm,动点P以1cm/s的速度从A点出发,经点D,C到点B,设△ABP的面积为s(cm2),点P运动的时间为t(s).
(1)求当点P在线段AD上时,s与t之间的函数关系式;
(2)求当点P在线段BC上时,s与t之间的函数关系式;