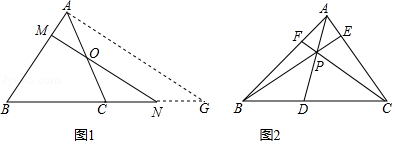
如图1所示,在 中,点 是 上一点,过点 的直线与 , 的延长线分别相交于点 , .
【问题引入】
(1)若点 是 的中点, ,求 的值;
温馨提示:过点 作 的平行线交 的延长线于点 .
【探索研究】
(2)若点 是 上任意一点(不与 , 重合),求证: ;
【拓展应用】
(3)如图2所示,点 是 内任意一点,射线 , , 分别交 , , 于点 , , ,若 , ,求 的值.
解不等式组:
如图,在平面直角坐标系中,直角三角形AOB的顶点A、B分别落在坐标轴上.O为原点,点A的坐标为(6,0),点B的坐标为(0,8).动点M从点O出发.沿OA向终点A以每秒1个单位的速度运动,同时动点N从点A出发,沿AB向终点B以每秒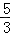 个单位的速度运动.当一个动点到达终点时,另一个动点也随之停止运动,设动点M、N运动的时间为t秒(t>0).
个单位的速度运动.当一个动点到达终点时,另一个动点也随之停止运动,设动点M、N运动的时间为t秒(t>0).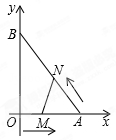
(1)当t=3秒时.直接写出点N的坐标,并求出经过O、A、N三点的抛物线的解析式;
(2)在此运动的过程中,△MNA的面积是否存在最大值?若存在,请求出最大值;若不存在,请说明理由;
(3)当t为何值时,△MNA是一个等腰三角形?
如图,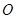 是坐标原点,过点
是坐标原点,过点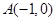 的抛物线
的抛物线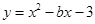 与
与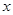 轴的另一个交点为
轴的另一个交点为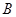 ,与
,与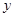 轴交于点
轴交于点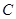 ,其顶点为
,其顶点为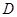 点.
点.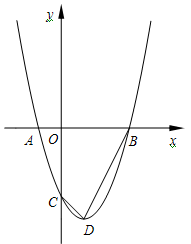
(1)求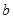 的值.
的值.
(2)连结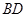 、
、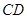 ,动点
,动点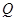 的坐标为
的坐标为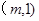 .
.
①当四边形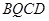 是平行四边形时,求
是平行四边形时,求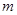 的值;
的值;
②连结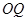 、
、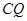 ,当
,当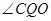 最大时,求出点
最大时,求出点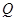 的坐标.
的坐标.
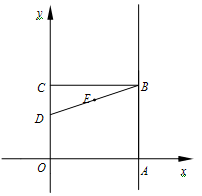
如图,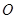 是坐标原点,矩形
是坐标原点,矩形 的顶点
的顶点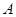 在
在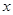 轴的正半轴上,点
轴的正半轴上,点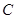 在
在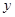 轴的正半轴上,点
轴的正半轴上,点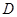 在边
在边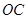 上,且点
上,且点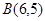 ,
,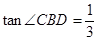 .
.
(1)填空: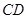 的长为;
的长为;
(2)若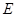 是
是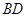 的中点,将过点
的中点,将过点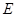 的直线
的直线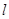 绕
绕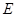 旋转,分别与直线
旋转,分别与直线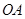 、
、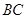 相交于点
相交于点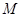 、
、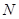 ,与直线
,与直线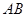 相交于点
相交于点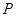 ,连结
,连结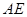 .
.
①设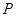 点的纵坐标为
点的纵坐标为 .当
.当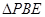 ∽
∽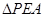 时,求
时,求 的值;
的值;
②试问:在旋转的过程中,线段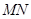 与
与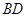 能否相等?若能,请求出
能否相等?若能,请求出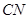 的长;若不能,请说明理由.
的长;若不能,请说明理由.
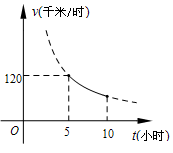
一辆客车从甲地出发前往乙地,平均速度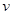 (千米/小时)与所用时间
(千米/小时)与所用时间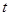 (小时)的函数关系如图所示,其中
(小时)的函数关系如图所示,其中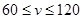 .
.
(1)直接写出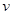 与
与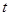 的函数关系式;
的函数关系式;
(2)若一辆货车同时从乙地出发前往甲地,客车比货车平均每小时多行驶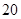 千米,
千米,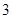 小时后两车相遇.
小时后两车相遇.
①求两车的平均速度;
②甲、乙两地间有两个加油站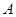 、
、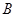 ,它们相距
,它们相距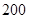 千米,当客车进入
千米,当客车进入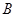 加油站时,货车恰好进入
加油站时,货车恰好进入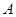 加油站(两车加油的时间忽略不计),求甲地与
加油站(两车加油的时间忽略不计),求甲地与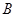 加油站的距离.
加油站的距离.